java.math.BigDecimal 加减乘除计算
Bigdecimal的初始化
这里对比了两种形式,第一种直接value写数字的值,第二种用string来表示
BigDecimal num1 = new BigDecimal(0.005);
BigDecimal num2 = new BigDecimal(1000000);
BigDecimal num3 = new BigDecimal(-1000000);
//尽量用字符串的形式初始化
BigDecimal num12 = new BigDecimal("0.005");
BigDecimal num22 = new BigDecimal("1000000");
BigDecimal num32 = new BigDecimal("-1000000");加减乘除绝对值的运算
其实就是Bigdecimal的类的一些调用
加法 add()函数
减法subtract()函数
乘法multiply()函数
除法divide()函数
绝对值abs()函数
我这里承接上面初始化Bigdecimal分别用string和数进行运算对比
//加法 BigDecimal result1 = num1.add(num2); BigDecimal result12 = num12.add(num22); //减法 BigDecimal result2 = num1.subtract(num2); BigDecimal result22 = num12.subtract(num22); //乘法 BigDecimal result3 = num1.multiply(num2); BigDecimal result32 = num12.multiply(num22); //绝对值 BigDecimal result4 = num3.abs(); BigDecimal result42 = num32.abs(); //除法 BigDecimal result5 = num2.divide(num1,20,BigDecimal.ROUND_HALF_UP); BigDecimal result52 = num22.divide(num12,20,BigDecimal.ROUND_HALF_UP);
我把result全部输出可以看到结果
这里出现了差异,这也是为什么初始化建议使用string的原因
※ 注意:
1)System.out.println()中的数字默认是double类型的,double类型小数计算不精准。
2)使用BigDecimal类构造方法传入double类型时,计算的结果也是不精确的!
因为不是所有的浮点数都能够被精确的表示成一个double 类型值,有些浮点数值不能够被精确的表示成 double 类型值,因此它会被表示成与它最接近的 double 类型的值。必须改用传入String的构造方法。这一点在BigDecimal类的构造方法注释中有说明。
完整的test代码如下:
import java.math.BigDecimal;
import java.util.Scanner;
public class TestThree {
public static void main(String[] args) {
BigDecimal num1 = new BigDecimal(0.005);
BigDecimal num2 = new BigDecimal(1000000);
BigDecimal num3 = new BigDecimal(-1000000);
//尽量用字符串的形式初始化
BigDecimal num12 = new BigDecimal("0.005");
BigDecimal num22 = new BigDecimal("1000000");
BigDecimal num32 = new BigDecimal("-1000000");
//加法
BigDecimal result1 = num1.add(num2);
BigDecimal result12 = num12.add(num22);
//减法
BigDecimal result2 = num1.subtract(num2);
BigDecimal result22 = num12.subtract(num22);
//乘法
BigDecimal result3 = num1.multiply(num2);
BigDecimal result32 = num12.multiply(num22);
//绝对值
BigDecimal result4 = num3.abs();
BigDecimal result42 = num32.abs();
//除法
BigDecimal result5 = num2.divide(num1,20,BigDecimal.ROUND_HALF_UP);
BigDecimal result52 = num22.divide(num12,20,BigDecimal.ROUND_HALF_UP);
System.out.println("加法用value结果:"+result1);
System.out.println("加法用string结果:"+result12);
System.out.println("减法value结果:"+result2);
System.out.println("减法用string结果:"+result22);
System.out.println("乘法用value结果:"+result3);
System.out.println("乘法用string结果:"+result32);
System.out.println("绝对值用value结果:"+result4);
System.out.println("绝对值用string结果:"+result42);
System.out.println("除法用value结果:"+result5);
System.out.println("除法用string结果:"+result52);
}
}除法divide()参数使用
使用除法函数在divide的时候要设置各种参数,要精确的小数位数和舍入模式,不然会出现报错
我们可以看到divide函数配置的参数如下
即为 (BigDecimal divisor 除数, int scale 精确小数位, int roundingMode 舍入模式)
可以看到舍入模式有很多种BigDecimal.ROUND_XXXX_XXX, 具体都是什么意思呢
计算1÷3的结果(最后一种ROUND_UNNECESSARY在结果为无限小数的情况下会报错)
八种舍入模式解释如下
1、ROUND_UP
舍入远离零的舍入模式。
在丢弃非零部分之前始终增加数字(始终对非零舍弃部分前面的数字加1)。
注意,此舍入模式始终不会减少计算值的大小。
2、ROUND_DOWN
接近零的舍入模式。
在丢弃某部分之前始终不增加数字(从不对舍弃部分前面的数字加1,即截短)。
注意,此舍入模式始终不会增加计算值的大小。
3、ROUND_CEILING
接近正无穷大的舍入模式。
如果 BigDecimal 为正,则舍入行为与 ROUND_UP 相同;
如果为负,则舍入行为与 ROUND_DOWN 相同。
注意,此舍入模式始终不会减少计算值。
4、ROUND_FLOOR
接近负无穷大的舍入模式。
如果 BigDecimal 为正,则舍入行为与 ROUND_DOWN 相同;
如果为负,则舍入行为与 ROUND_UP 相同。
注意,此舍入模式始终不会增加计算值。
5、ROUND_HALF_UP
向“最接近的”数字舍入,如果与两个相邻数字的距离相等,则为向上舍入的舍入模式。
如果舍弃部分 >= 0.5,则舍入行为与 ROUND_UP 相同;否则舍入行为与 ROUND_DOWN 相同。
注意,这是我们大多数人在小学时就学过的舍入模式(四舍五入)。
6、ROUND_HALF_DOWN
向“最接近的”数字舍入,如果与两个相邻数字的距离相等,则为上舍入的舍入模式。
如果舍弃部分 > 0.5,则舍入行为与 ROUND_UP 相同;否则舍入行为与 ROUND_DOWN 相同(五舍六入)。
7、ROUND_HALF_EVEN
向“最接近的”数字舍入,如果与两个相邻数字的距离相等,则向相邻的偶数舍入。
如果舍弃部分左边的数字为奇数,则舍入行为与 ROUND_HALF_UP 相同;
如果为偶数,则舍入行为与 ROUND_HALF_DOWN 相同。
注意,在重复进行一系列计算时,此舍入模式可以将累加错误减到最小。
此舍入模式也称为“银行家舍入法”,主要在美国使用。四舍六入,五分两种情况。
如果前一位为奇数,则入位,否则舍去。
以下例子为保留小数点1位,那么这种舍入方式下的结果。
1.15>1.2 1.25>1.2
8、ROUND_UNNECESSARY
断言请求的操作具有精确的结果,因此不需要舍入。
如果对获得精确结果的操作指定此舍入模式,则抛出ArithmeticException。
完美解决Non-terminating decimal expansion; no exact representable decimal result.异常
我们在使用BigDecimal进行精确计算时常常会出现Non-terminating decimal expansion; no exact representable decimal result.异常。
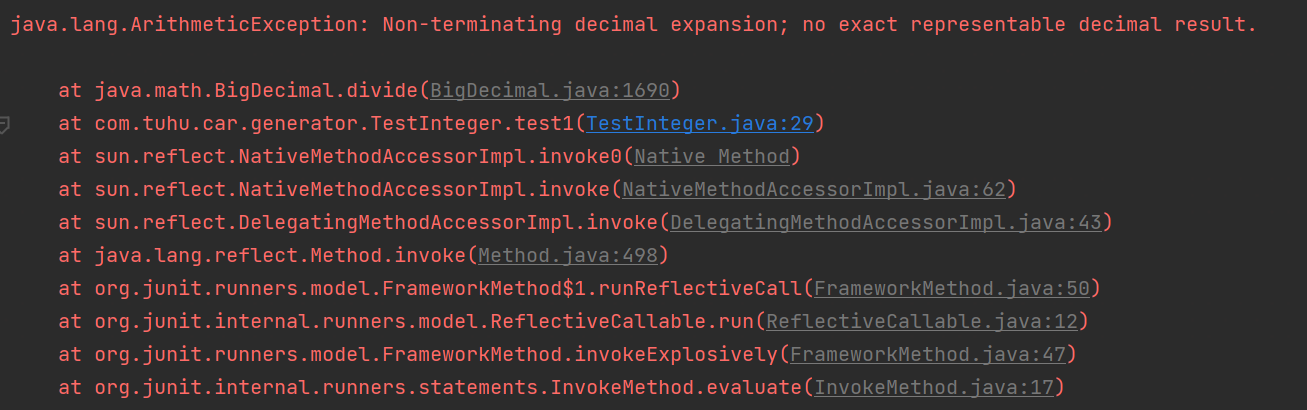
出现这个异常的原因在于 BigDecimal 是不可变的、任意精度的有符号十进制数,所以可以做精确计算。但在除法中,准确的商可能是一个无限长的十进制扩展;例如,1 除以 3 所得的商。我们在做除法时,没有指定舍入模式,并且无法表示为准确的结果,因此抛出了这个异常(java.lang.ArithmeticException)。
知道了原因我们该如何解决呢?
只需要在 divide() 方法中传入 MathContext 对象或 RoundingMode 对象,指定精度和舍入模式就可以解决该问题。
RoundingMode 对象的八种舍入模式
常量名 说明
CEILING 向正无限大方向舍入
DOWN 向零方向舍入
FLOOR 向负无限大方向舍入
HALF_DOWN 向最接近数字方向舍入,如果与两个相邻数字的距离相等,则向下舍入
HALF_EVEN 向最接近数字方向舍入,如果与两个相邻数字的距离相等,则向相邻的偶数舍入
HALF_UP 向最接近数字方向舍入,如果与两个相邻数字的距离相等,则向上舍入
UNNECESSARY 断言具有精确结果
这里要根据业务选择合适的方法没有最好的只有最适合的。本文采用的是在divide运算时指定保留两位小数点的方法解决。详情看下图。

修改完成后经测试。该问题成功解决!
原文链接: https://www.yukx.com/xiaomengbao/article/details/2369.html 优科学习网java.math.BigDecimal 加减乘除计算
-
 雪花算法(Snowflake)是由Twitter开发的一种分布式ID生成算法,旨在为分布式系统提供一种简单而有效的方式,以生成全局唯一、有序且可排序的64位整数ID。这种ID通常用作数据库记录的主键或其他需要唯一标识符的场景。雪花算法生成的64位ID结构如下:最高位(第64位):固定为0,因为64位
雪花算法(Snowflake)是由Twitter开发的一种分布式ID生成算法,旨在为分布式系统提供一种简单而有效的方式,以生成全局唯一、有序且可排序的64位整数ID。这种ID通常用作数据库记录的主键或其他需要唯一标识符的场景。雪花算法生成的64位ID结构如下:最高位(第64位):固定为0,因为64位 -
 在HTML中,如果你想让一个输入框(input元素)不可编辑,你可以通过设置其readonly属性来实现。示例如下:input type="text" value="此处内容不可编辑" readonly在上述代码中,readonly属性使得用户无法修改输入框中的内容。另外,如果你希望输入框完全不可交
在HTML中,如果你想让一个输入框(input元素)不可编辑,你可以通过设置其readonly属性来实现。示例如下:input type="text" value="此处内容不可编辑" readonly在上述代码中,readonly属性使得用户无法修改输入框中的内容。另外,如果你希望输入框完全不可交 -
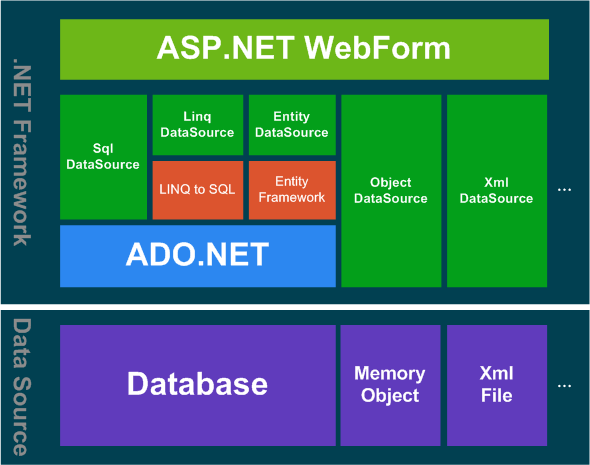 ASP.NET教程ASP.NET又称为ASP+,基于.NETFramework的Web开发平台,是微软公司推出的新一代脚本语言。ASP.NET是一个使用HTML、CSS、JavaScript和服务器脚本创建网页和网站的开发框架。ASP.NET支持三种不一样的开发模式:WebPages(Web页面)、
ASP.NET教程ASP.NET又称为ASP+,基于.NETFramework的Web开发平台,是微软公司推出的新一代脚本语言。ASP.NET是一个使用HTML、CSS、JavaScript和服务器脚本创建网页和网站的开发框架。ASP.NET支持三种不一样的开发模式:WebPages(Web页面)、 -
 C# 判断判断结构要求程序员指定一个或多个要评估或测试的条件,以及条件为真时要执行的语句(必需的)和条件为假时要执行的语句(可选的)。下面是大多数编程语言中典型的判断结构的通常形式:判断语句C#提供了以下类型的判断语句。点击链接查看每个语句的细节。语句描述if语句一个 if语句 由一个布尔表达式后跟
C# 判断判断结构要求程序员指定一个或多个要评估或测试的条件,以及条件为真时要执行的语句(必需的)和条件为假时要执行的语句(可选的)。下面是大多数编程语言中典型的判断结构的通常形式:判断语句C#提供了以下类型的判断语句。点击链接查看每个语句的细节。语句描述if语句一个 if语句 由一个布尔表达式后跟 -
 C#循环有的时候,可能需要多次执行同一块代码。通常情况下,语句是顺序执行的:函数中的第一个语句先执行,接着是第二个语句,依此类推。编程语言提供了允许更为复杂的执行路径的多种控制结构。循环语句允许我们多次执行一个语句或语句组,下面是大多数编程语言中循环语句的通常形式:循环类型C#提供了以下几种循环类型
C#循环有的时候,可能需要多次执行同一块代码。通常情况下,语句是顺序执行的:函数中的第一个语句先执行,接着是第二个语句,依此类推。编程语言提供了允许更为复杂的执行路径的多种控制结构。循环语句允许我们多次执行一个语句或语句组,下面是大多数编程语言中循环语句的通常形式:循环类型C#提供了以下几种循环类型 -
 C#数组(Array)数组是一个存储相同类型元素的固定大小的顺序集合。数组是用来存储数据的集合,一般认为数组是一个同一类型变量的集合。声明数组变量并不是声明number0、number1、...、number99一个个单独的变量,而是声明一个就像numbers这样的变量,然后使用numbers[0]
C#数组(Array)数组是一个存储相同类型元素的固定大小的顺序集合。数组是用来存储数据的集合,一般认为数组是一个同一类型变量的集合。声明数组变量并不是声明number0、number1、...、number99一个个单独的变量,而是声明一个就像numbers这样的变量,然后使用numbers[0]

