剪枝算法
剪枝算法在不同的上下文中有不同的含义:
决策树剪枝算法 在机器学习领域,尤其是决策树模型中,剪枝算法主要用于防止过拟合,通过削减过于复杂的决策树来提高模型的泛化能力。常见的决策树剪枝策略包括预剪枝(Pre-pruning)和后剪枝(Post-pruning):
预剪枝:在构建决策树过程中,通过提前停止树的增长(例如限制树的最大深度、叶节点最少样本数、信息增益阈值等)来防止过拟合。
后剪枝:先构建一棵完整的决策树,然后从底部向上检查每个非叶子节点,若替换为该节点的子树能够带来更高的泛化性能,则将该节点及其子树剪掉。
模型压缩中的剪枝算法 在深度学习和神经网络领域,模型剪枝是指为了减小模型大小、加速推理速度而采取的一种模型压缩手段。它通过移除网络中的一些权重(权重剪枝)或者整个神经元及连接(结构剪枝),使模型变得更加稀疏。例如:
单元剪枝(Neuron Pruning):丢弃神经网络中激活值较小的神经元。
连接剪枝(Connection Pruning):删除权值接近于0或绝对值较小的权重连接。
更高级的剪枝策略包括Dropout、DropConnect、Lottery Ticket Hypothesis等。
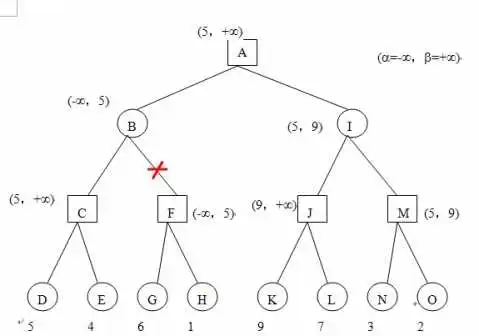
搜索算法中的剪枝 在棋类游戏或搜索问题中,剪枝算法是指在搜索树中排除那些不可能导致最优解或者明显劣于当前已知最佳解的子树,以减少搜索空间,提高搜索效率。例如Alpha-Beta剪枝算法,该算法基于Minimax搜索框架,在Alpha-beta搜索过程中利用alpha和beta边界值来剪去不会影响最终决策的子节点。
具体的剪枝算法如CART(Classification and Regression Trees)中的Cost Complexity Pruning,通过计算每个节点的信息增益比以及惩罚项,决定是否剪枝。
综上所述,剪枝算法是一种优化技术,根据不同场景和需求,通过剔除冗余或低效的部分来改善算法性能或资源占用。
剪枝算法应用场景
剪枝算法的应用场景较多,这里提供一个简单的决策树剪枝算法的Java示例(使用ID3算法)以及一个深度学习权重剪枝的Java思路概述:
决策树剪枝示例(ID3算法基础上的后剪枝)
// ID3决策树后剪枝的简化版伪代码,实际实现会更复杂,涉及大量类和方法
class DecisionTree {
Node root;
// ... 构建决策树的方法省略 ...
// 后剪枝的简略实现
void postPrune(Node node, double alpha) {
if (node.isLeaf()) {
return;
}
// 递归剪枝子节点
for (Node child : node.children) {
postPrune(child, alpha);
}
// 计算剪枝后误差率
double errorWithoutNode = calculateError(node.children);
double errorWithNode = calculateError(node);
// 若剪枝后误差率更低,则剪枝
if (errorWithoutNode <= errorWithNode * Math.pow(alpha, node.depth)) {
node.isLeaf = true;
node.value = majorityVote(node.children);
}
}
// 计算子树误差率和多数类别投票的方法省略 ...
}
class Node {
boolean isLeaf;
List<Node> children;
int depth;
String value; // 叶子节点的类别标签
// ... 其他属性和方法省略 ...
}深度学习权重剪枝示例思路
在深度学习中,权重剪枝通常涉及到将权重矩阵中的较小权重置零,并在网络训练过程中保持稀疏性。以下是一个简化的Java描述,实际实现中可能使用TensorFlow、PyTorch等库进行操作:
// 假设WeightMatrix是一个包装了权重矩阵的类
class WeightMatrix {
double[][] weights;
// 假设threshold为设定的阈值,prune方法将低于阈值的权重置零
void prune(double threshold) {
for (int i = 0; i < weights.length; i++) {
for (int j = 0; j < weights[i].length; j++) {
if (Math.abs(weights[i][j]) < threshold) {
weights[i][j] = 0.0;
}
}
}
}
// 进一步的,还需要配合训练过程动态调整阈值、恢复部分重要权重等操作
// ... 实际实现会更为复杂,可能结合Magnitude-based pruning, Lottery Ticket Hypothesis等方法 ...
}
// 使用时,调用剪枝方法
WeightMatrix layerWeights;
double threshold = determineThreshold(); // 根据训练进度和策略确定阈值
layerWeights.prune(threshold);请注意,实际的深度学习权重剪枝代码会更为复杂,涉及到具体的模型训练、反向传播、稀疏梯度更新、模型微调等多个环节,并且通常需要集成到深度学习框架中实现。上述代码仅为简化的示意,实际开发中应参考现有深度学习库提供的接口和API。
原文链接: https://www.yukx.com/arithmetic/article/details/2476.html 优科学习网剪枝算法
-
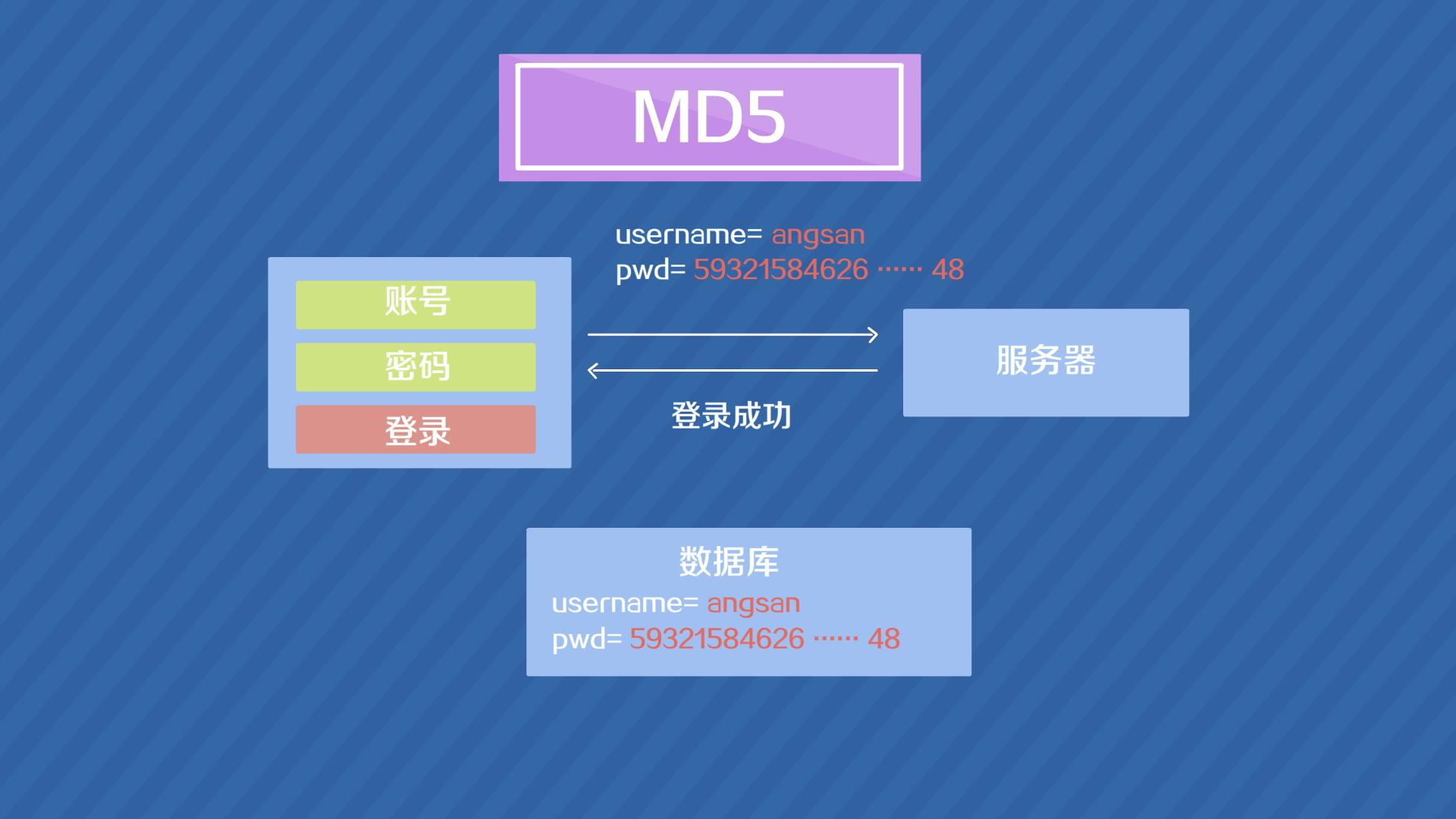 MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到
MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到 -
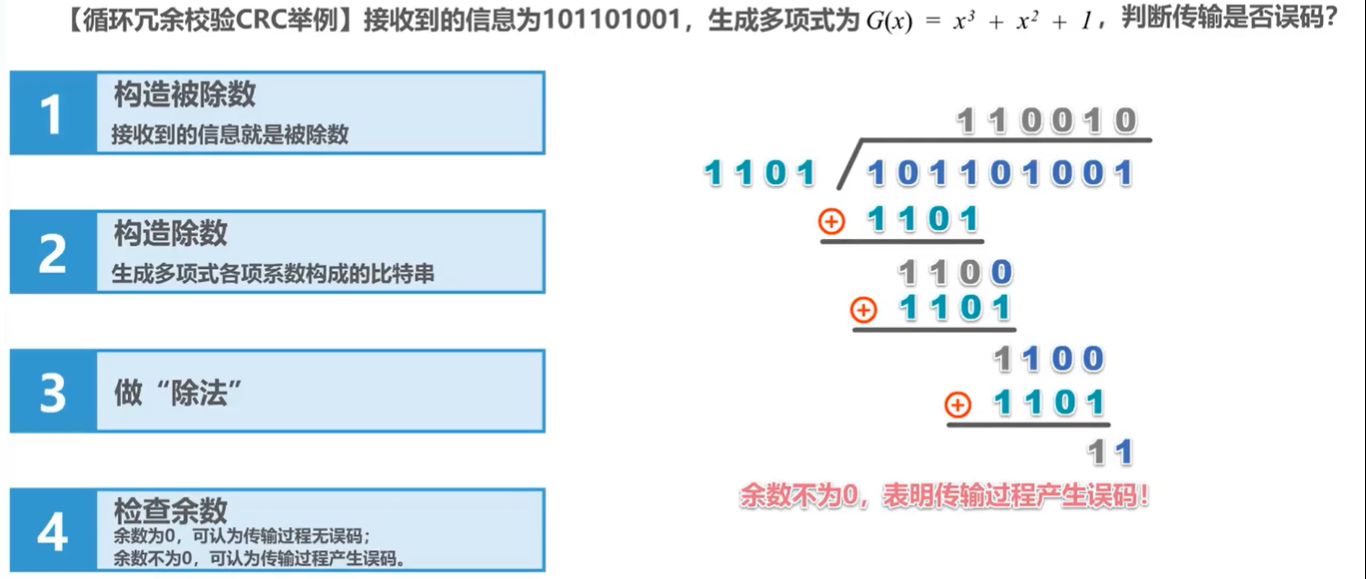 循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确
循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确 -
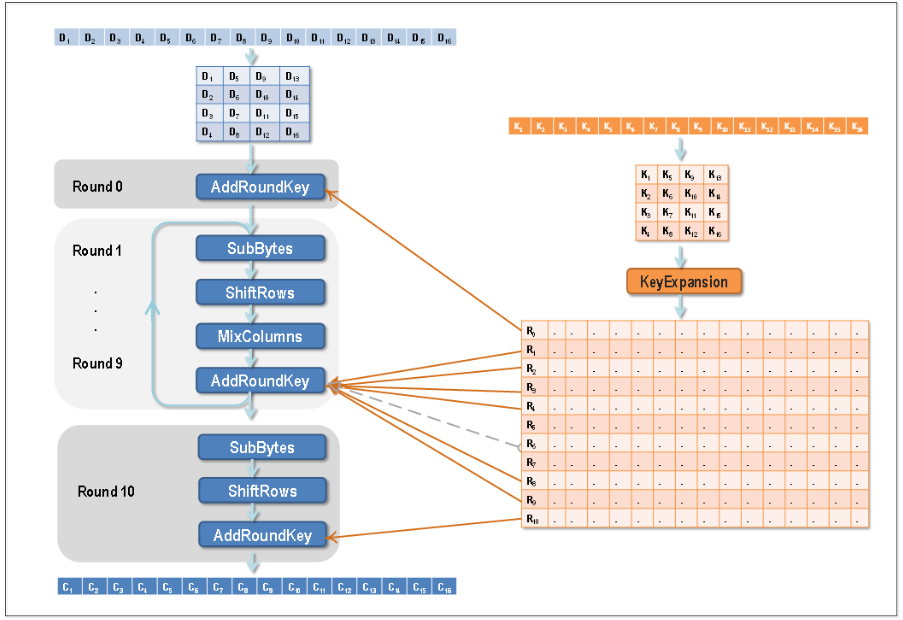 AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛
AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛 -
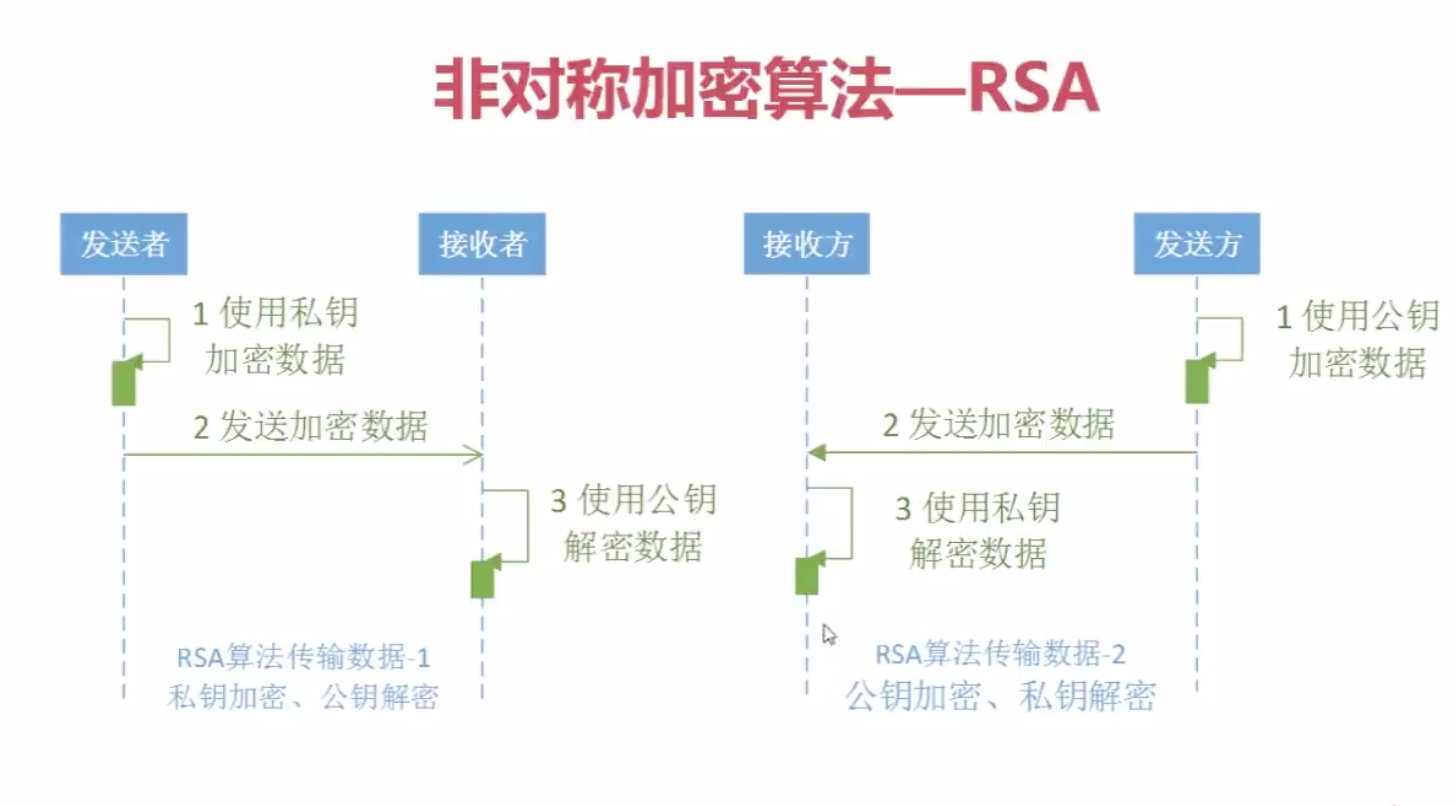 RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难
RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难 -
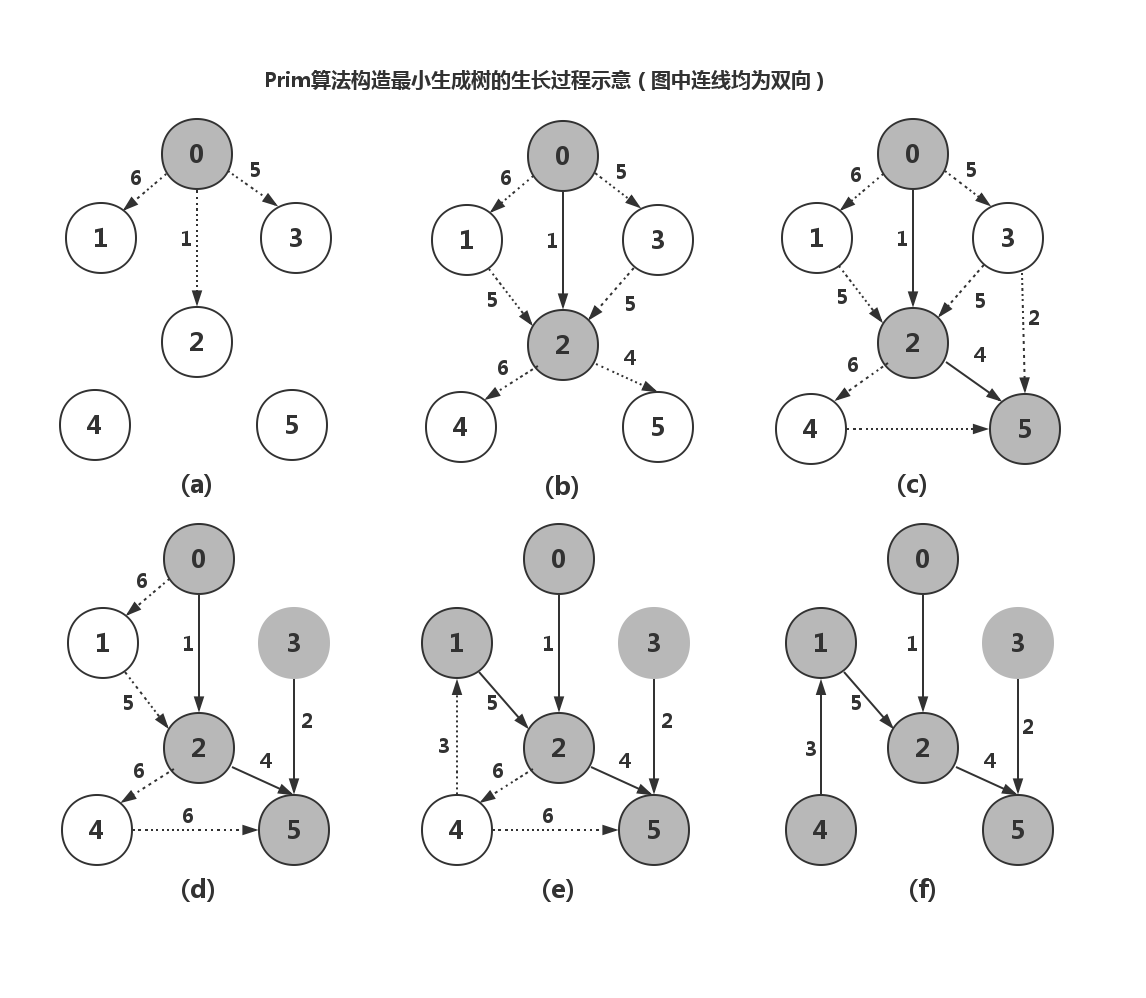 最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添
最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添 -
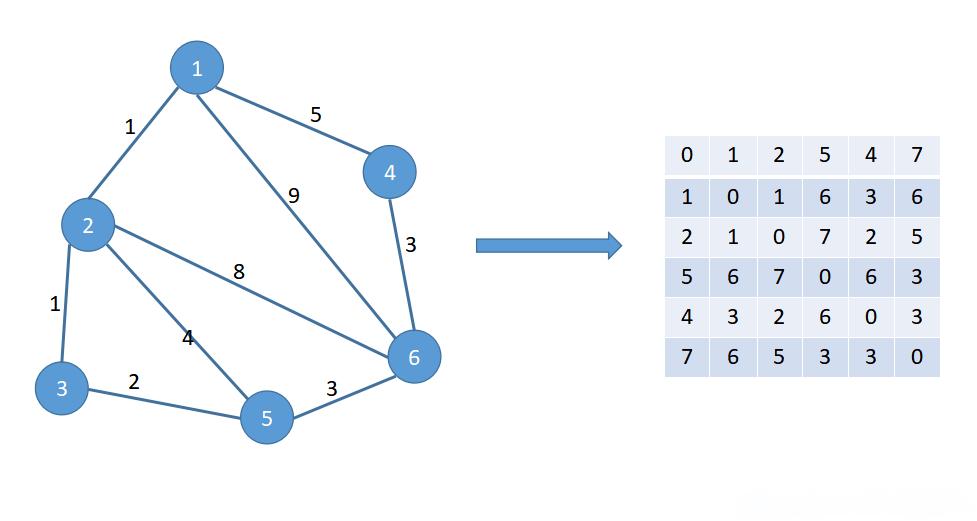 关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选
关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选

