最小生成树算法
最小生成树(Minimum Spanning Tree, MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。
Prim算法
原理: Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添加一条与已选顶点集相连且权重最小的边,直到所有的顶点都被包含进来为止。
步骤:
选择一个顶点作为起始点,将其标记为已选入生成树。
初始化一个优先队列(通常用最小堆实现),存储未被选入生成树的顶点与当前已选顶点集合中最近顶点的连线及其权重。
循环执行以下操作,直到所有顶点都被包含:
从优先队列中取出权重最小的边,这条边的一端属于已选顶点集合,另一端尚未被选入。
将这条边的未被选入的一端顶点加入已选顶点集合,并更新与新加入顶点相连的所有边在优先队列中的位置。
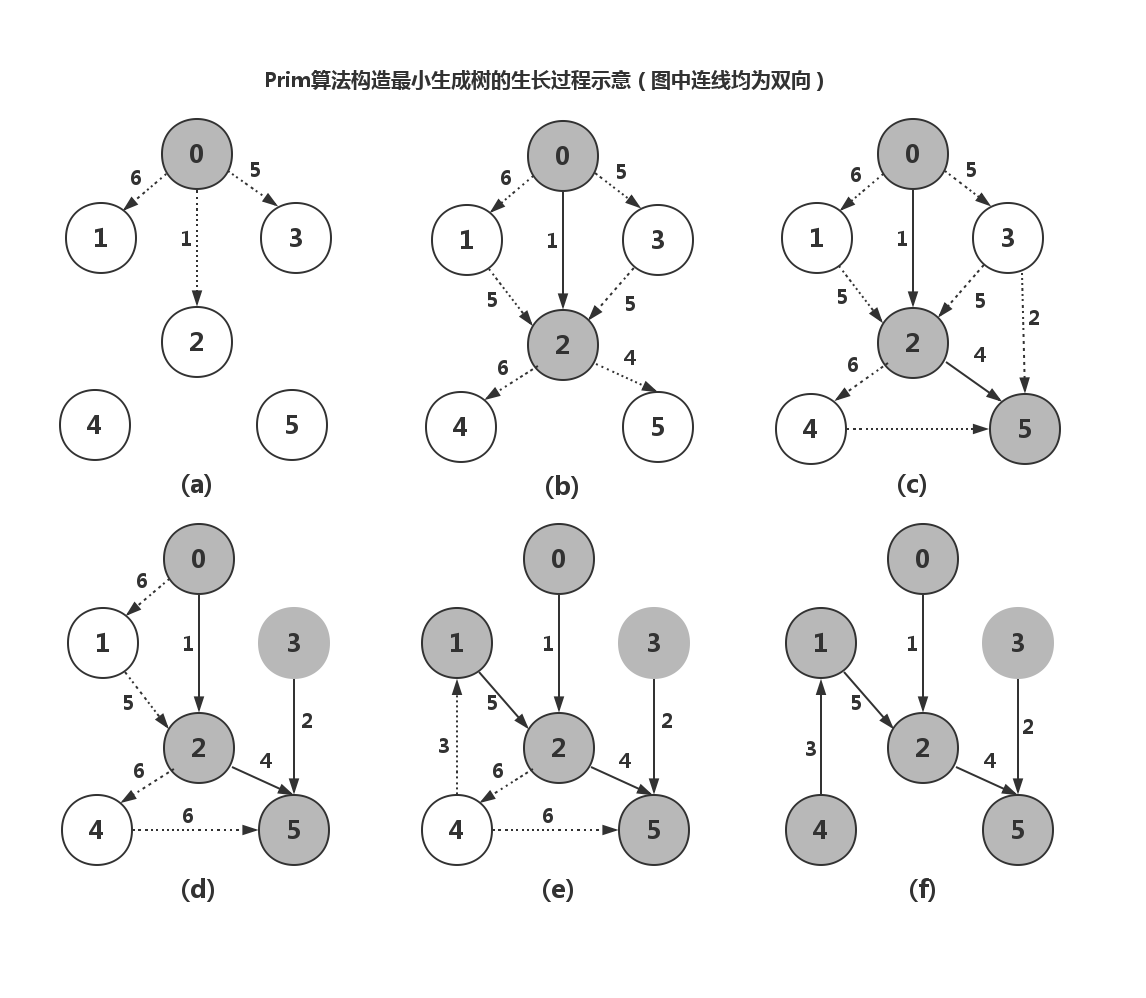
由于Prim算法在Java中实现通常涉及优先队列(如PriorityQueue)配合邻接矩阵或邻接表的数据结构,以下是一个基于邻接矩阵实现Prim算法的基本示例:
import java.util.*;
class Edge implements Comparable<Edge> {
int src;
int dest;
double weight;
Edge(int src, int dest, double weight) {
this.src = src;
this.dest = dest;
this.weight = weight;
}
@Override
public int compareTo(Edge other) {
return Double.compare(this.weight, other.weight);
}
}
public class PrimMST {
// Function to find MST using Prim's algorithm
public ArrayList<Edge> primMST(int[][] graph, int V) {
// Array to store constructed MST
ArrayList<Edge> result = new ArrayList<>();
// Boolean array to track vertices included in MST
boolean[] included = new boolean[V];
Arrays.fill(included, false);
// Include first vertex and initialize min heap
included[0] = true;
PriorityQueue<Edge> minHeap = new PriorityQueue<>(new Comparator<Edge>() {
@Override
public int compare(Edge e1, Edge e2) {
return Double.compare(e1.weight, e2.weight);
}
});
// Add all edges from the first vertex to the min heap
for (int v = 1; v < V; v++) {
if (graph[0][v] != 0)
minHeap.add(new Edge(0, v, graph[0][v]));
}
while (!minHeap.isEmpty()) {
// Extract the minimum edge
Edge currentEdge = minHeap.poll();
int u = currentEdge.src;
int v = currentEdge.dest;
// If destination vertex is not already included, add it to MST and update min heap
if (!included[v]) {
included[v] = true;
result.add(currentEdge); // Add this edge to the MST
// Relax all edges connected to the newly added vertex
for (int w = 0; w < V; w++) {
if (!included[w] && graph[v][w] != 0)
minHeap.add(new Edge(v, w, graph[v][w]));
}
}
}
return result;
}
public static void main(String[] args) {
int V = 5; // Number of vertices
int[][] graph = {
{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0}
};
PrimMST prim = new PrimMST();
ArrayList<Edge> mst = prim.primMST(graph, V);
// Print MST edges
for (Edge e : mst)
System.out.println("Edge (" + e.src + ", " + e.dest + ") with weight " + e.weight);
}
}这个示例中,Edge类表示图中的每一条边,包含源顶点、目标顶点和权重。primMST方法实现了Prim算法的主要逻辑,它首先选择一个顶点并将与之相连的所有边放入优先队列中,然后每次从优先队列中取出权值最小的边,并检查其终点是否已经加入到最小生成树中,若是则忽略此边,否则添加此边到结果列表中并继续松弛其余未访问过的顶点对应的边。
请注意,上述代码适用于无向图。对于有向图,需要确保对称性(如果从u到v有一条边,那么从v到u也应该有一条相同的边)。另外,这个例子假设图是完全图,对于非完全图,需要在添加边进队列前检查是否存在相应的边及其权重不为0。
Kruskal算法
原理: Kruskal算法也是贪心算法,但它的策略是按照边的权重从小到大排序所有边,然后依次选取边,保证选取的边不会构成环。
步骤:
对图中所有边按权重升序排序。
初始化一个空集合用来存放已经加入最小生成树的边。
遍历排序后的边,对每条边检查是否与当前已加入集合的边构成环。若不构成环,则将该边加入集合中。
继续这个过程,直到加入的边数等于顶点数减一(因为树有n个顶点就有n-1条边)。
以下是Kruskal算法在Java中的实现示例,包括一个简单的Edge类以及KruskalMST类来计算加权无向图的最小生成树。为了处理可能形成的环,我们还需要实现一个并查集(Disjoint-Set Union, DSU)数据结构来进行集合操作。
import java.util.*;
class Edge implements Comparable<Edge> {
int src;
int dest;
double weight;
Edge(int src, int dest, double weight) {
this.src = src;
this.dest = dest;
this.weight = weight;
}
@Override
public int compareTo(Edge other) {
return Double.compare(this.weight, other.weight);
}
}
class DisjointSetUnion {
int[] parent;
int[] rank;
DisjointSetUnion(int n) {
parent = new int[n];
rank = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
rank[i] = 1;
}
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
rank[rootY] += rank[rootX];
} else {
parent[rootY] = rootX;
rank[rootX] += rank[rootY];
}
}
}
}
public class KruskalMST {
public List<Edge> kruskalMST(int[][] graph, int V) {
Arrays.sort(graph, (a1, a2) -> Double.compare(a1[2], a2[2])); // Sort edges by weight
DisjointSetUnion dsu = new DisjointSetUnion(V);
List<Edge> mst = new ArrayList<>();
for (int i = 0; i < V * (V - 1) / 2; i++) {
int u = graph[i][0];
int v = graph[i][1];
double weight = graph[i][2];
// Skip if same endpoint or duplicate edge
if (u == v)
continue;
// Check if adding this edge forms a cycle
if (dsu.find(u) != dsu.find(v)) {
mst.add(new Edge(u, v, weight));
dsu.union(u, v);
}
}
return mst;
}
public static void main(String[] args) {
int V = 5; // Number of vertices
int[][] graph = {
{0, 1, 4},
{0, 2, 3},
{0, 3, 2},
{1, 2, 1},
{1, 3, 6},
{1, 4, 5},
{2, 3, 1},
{2, 4, 4},
{3, 4, 3}
};
KruskalMST kruskal = new KruskalMST();
List<Edge> mst = kruskal.kruskalMST(graph, V);
// Print MST edges
for (Edge e : mst)
System.out.println("Edge (" + e.src + ", " + e.dest + ") with weight " + e.weight);
}
}这段代码首先将所有边按照权值排序,然后遍历这些边,对于每条边,通过并查集判断两个顶点是否已经在同一个集合中(即是否形成了环),如果不是,则将它们合并到同一个集合中,并将边添加到最小生成树的结果集中。当收集到V-1条边时,就构建好了最小生成树。
总结
这两种算法都可以正确地构建最小生成树,并且在不同的图结构中可能会有不同的效率表现。例如,Prim算法在稠密图中性能较好,而Kruskal算法在稀疏图尤其是存在大量小权重边的情况下更为高效,因为它不需要维护整个顶点集的邻接关系。
原文链接: https://www.yukx.com/arithmetic/article/details/2479.html 优科学习网最小生成树算法
-
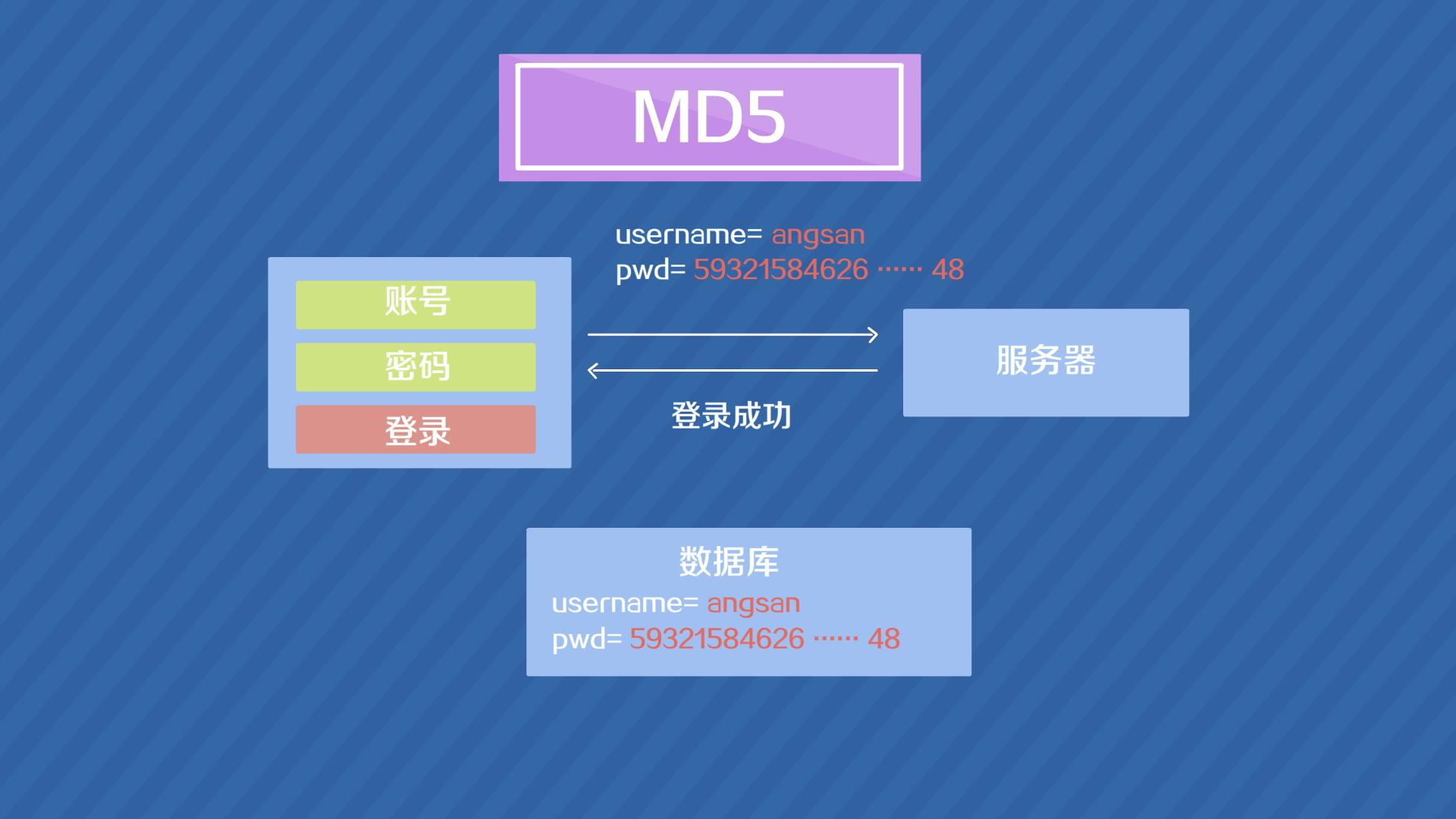 MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到
MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到 -
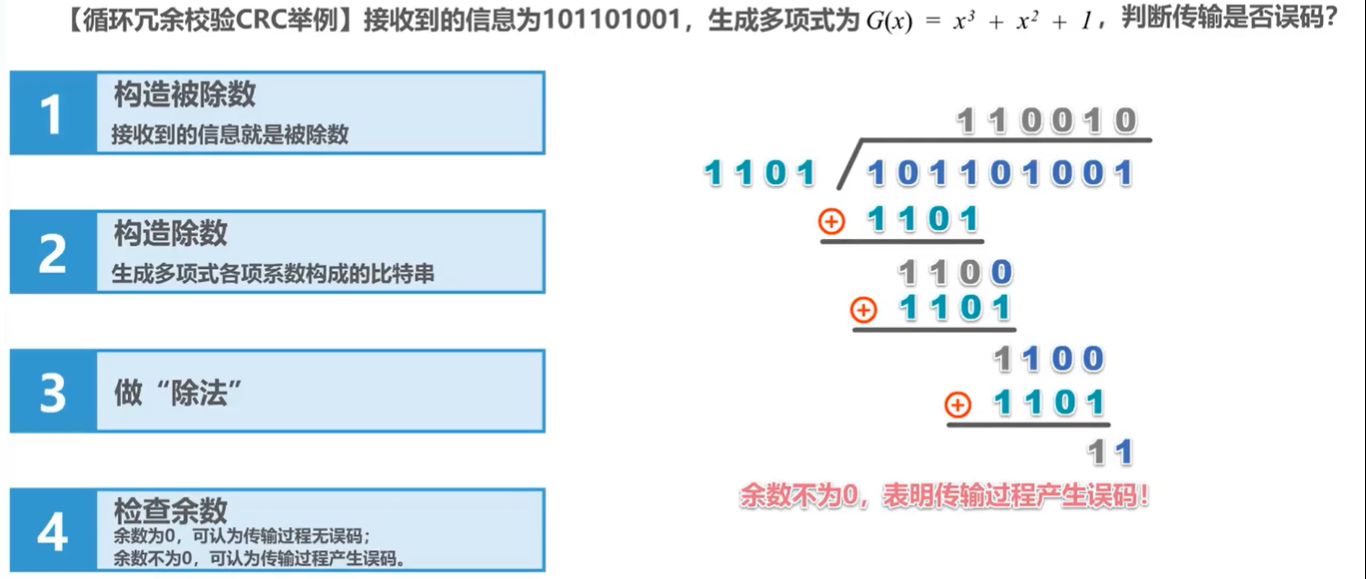 循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确
循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确 -
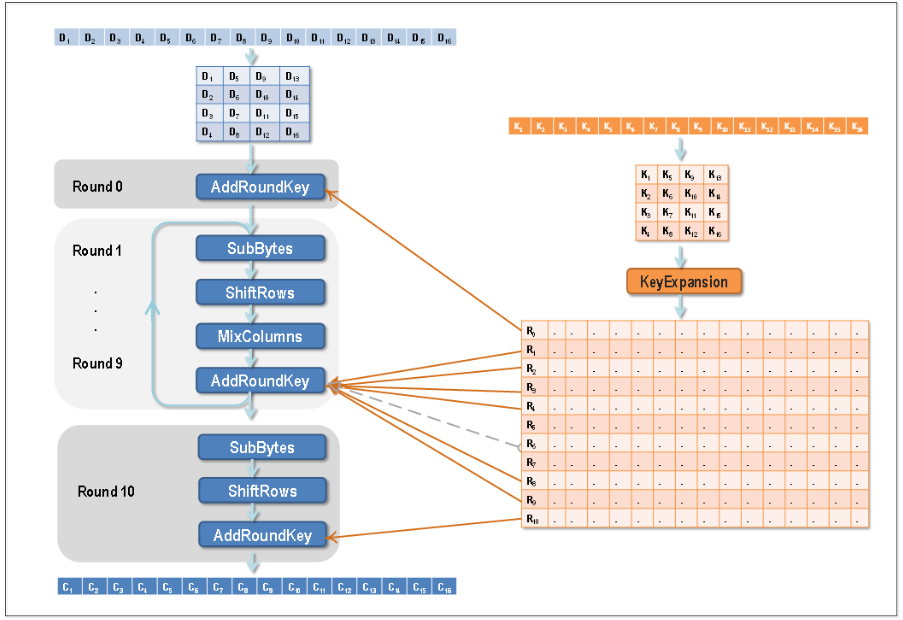 AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛
AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛 -
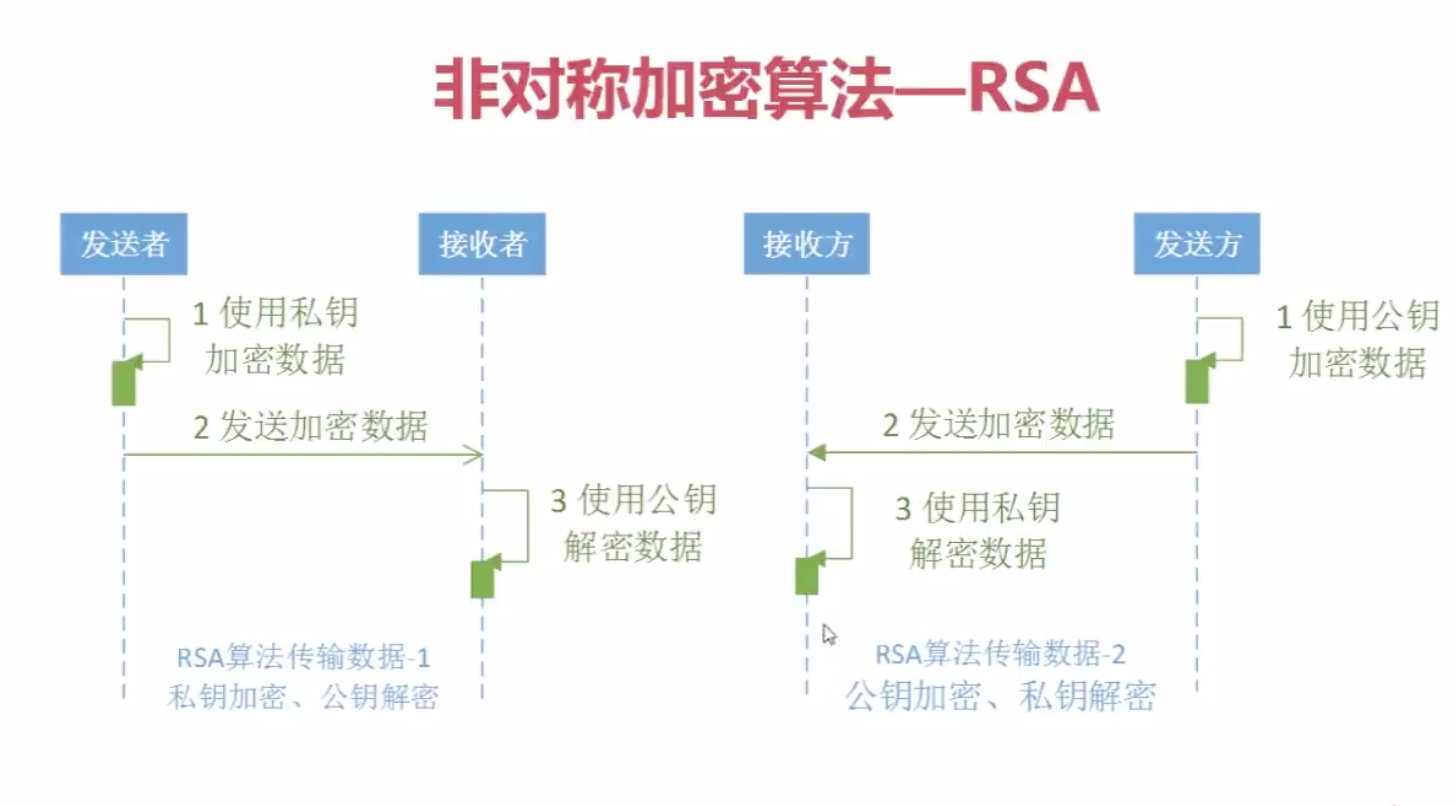 RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难
RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难 -
 最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添
最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添 -
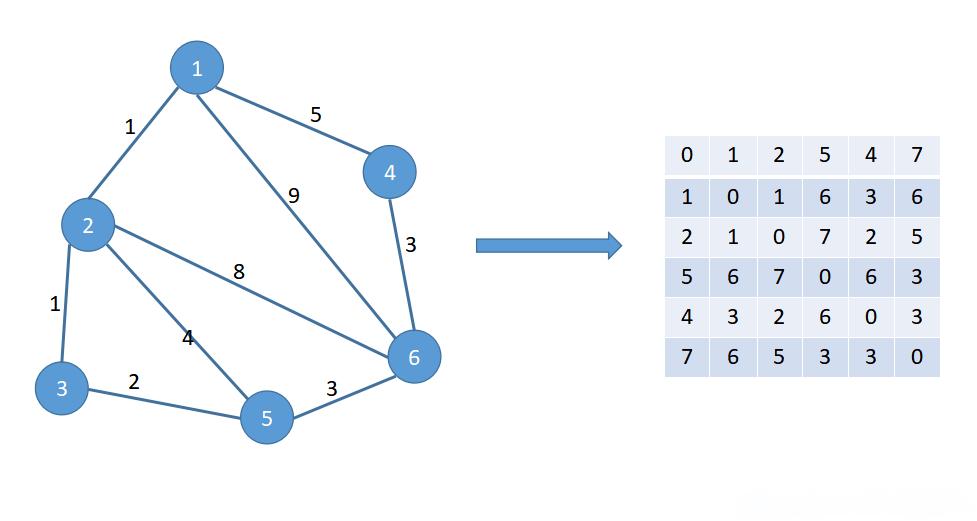 关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选
关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选

