回溯算法
回溯算法(Backtracking Algorithm)是一种用于解决约束满足问题(Constraint Satisfaction Problems,简称CSPs)和组合优化问题的有效算法策略。它是一种试探性的搜索算法,通过尝试在解空间中构建解决方案,并通过递归地尝试可能的选项来搜索解空间树,当遇到不满足约束条件的情况时,算法会撤销(回溯)至上一个分支点,尝试其他的路径。
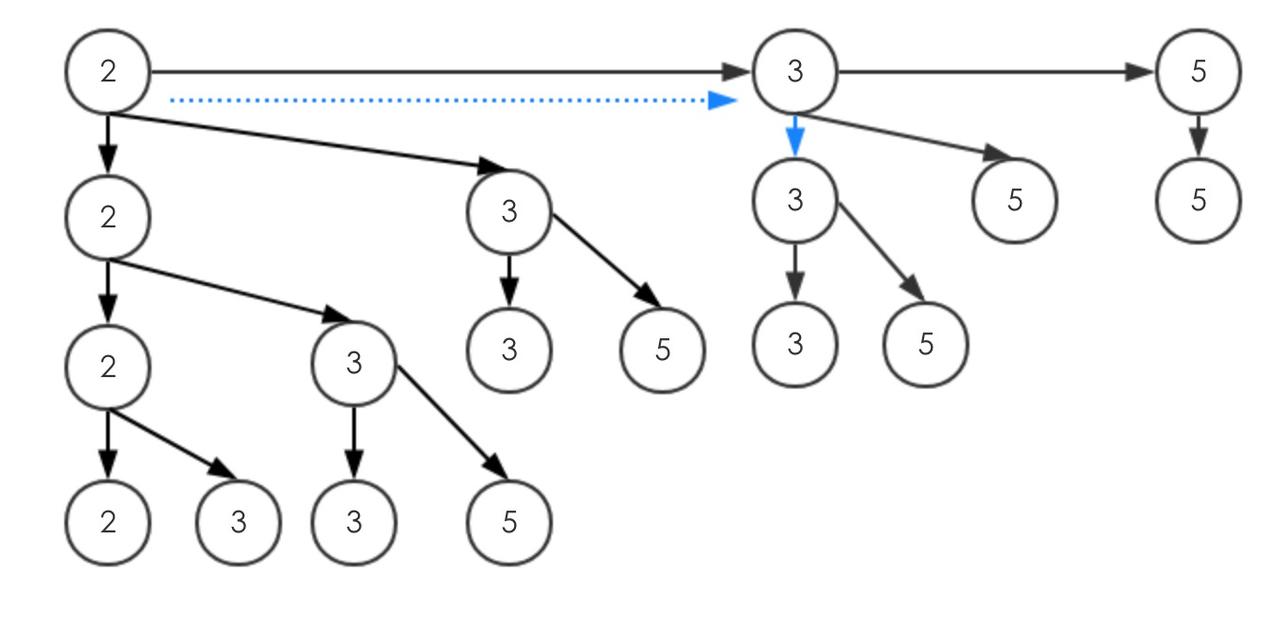
回溯算法的基本流程如下:
定义解空间:明确问题的解空间,即所有可能的解构成的集合。
初始状态:设定一个初始解的状态,通常是空解或者一个起点。
递归搜索:按照一定的策略(例如深度优先搜索)递归地扩展当前解,尝试添加新的元素或者修改当前解的状态。
满足约束:检查当前解是否满足问题的所有约束条件。如果满足,检查是否达到最终解的状态(如是否已经找到完整解),如果是则返回当前解;如果不是,则继续递归搜索。
不满足约束:如果不满足约束条件,则回溯(撤销最近一次的决策),即从解空间树中撤回到上一层节点,尝试其他可能的选项。
终止条件:当解空间中所有可能的解都被尝试过,并且没有找到符合条件的解时,算法结束。
回溯算法常见应用于多种问题,如八皇后问题、旅行商问题、数独问题、子集和问题、全排列问题、迷宫问题等等。在Java等编程语言中实现时,通常会借助递归函数和栈的数据结构来帮助追踪和回溯解空间树。
下面是一个使用回溯算法在Java中实现的全排列问题的代码示例:
import java.util.ArrayList;
import java.util.List;
public class Permutations {
public static List<List<Integer>> permute(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
backtrack(result, new ArrayList<>(), nums);
return result;
}
private static void backtrack(List<List<Integer>> result, List<Integer> tempList, int[] nums) {
// 基本情况:所有数字都已经填入排列中
if (tempList.size() == nums.length) {
result.add(new ArrayList<>(tempList));
return;
}
// 选择:尝试将nums中的每一个数字填入排列
for (int i = 0; i < nums.length; i++) {
// 跳过已经在排列中的数字
if (tempList.contains(nums[i])) {
continue;
}
// 执行:将当前数字填入排列
tempList.add(nums[i]);
// 探索:继续填入剩余数字
backtrack(result, tempList, nums);
// 撤销:将当前数字从排列中移除,以便尝试下一个数字
tempList.remove(tempList.size() - 1);
}
}
public static void main(String[] args) {
int[] nums = {1, 2, 3};
List<List<Integer>> permutations = permute(nums);
for (List<Integer> permutation : permutations) {
System.out.println(permutation);
}
}
}这段代码演示了如何使用回溯算法生成一个整数数组的所有可能全排列。backtrack 方法负责核心的回溯逻辑,通过递归调用自身来尝试所有可能的数字组合。当所有数字都被成功填入排列时,将当前排列添加到结果集中,并通过回溯机制恢复到上一层状态,继续尝试其他排列可能性。最后,程序会输出给定数组的所有全排列。
原文链接: https://www.yukx.com/arithmetic/article/details/2477.html 优科学习网回溯算法
-
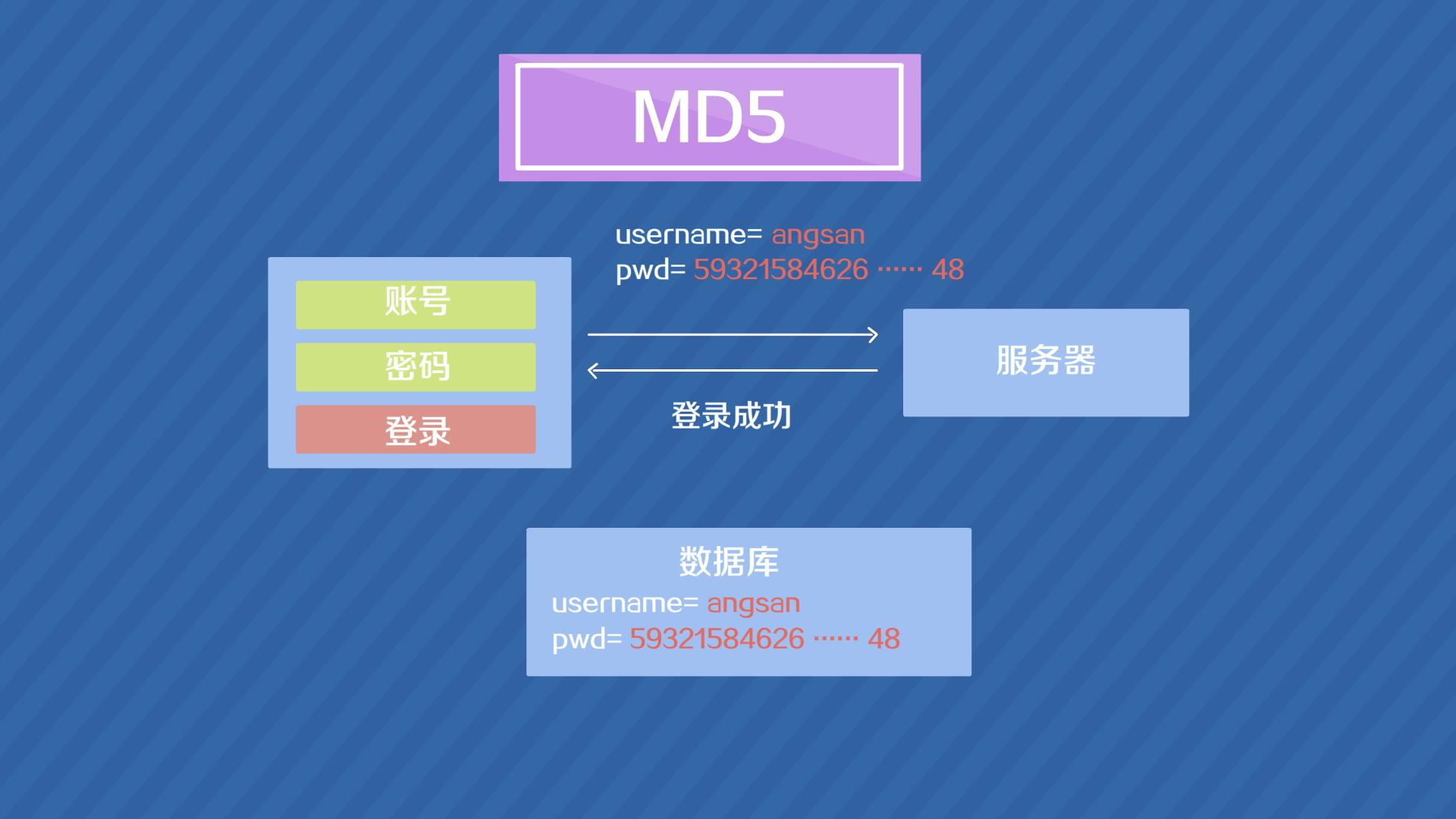 MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到
MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到 -
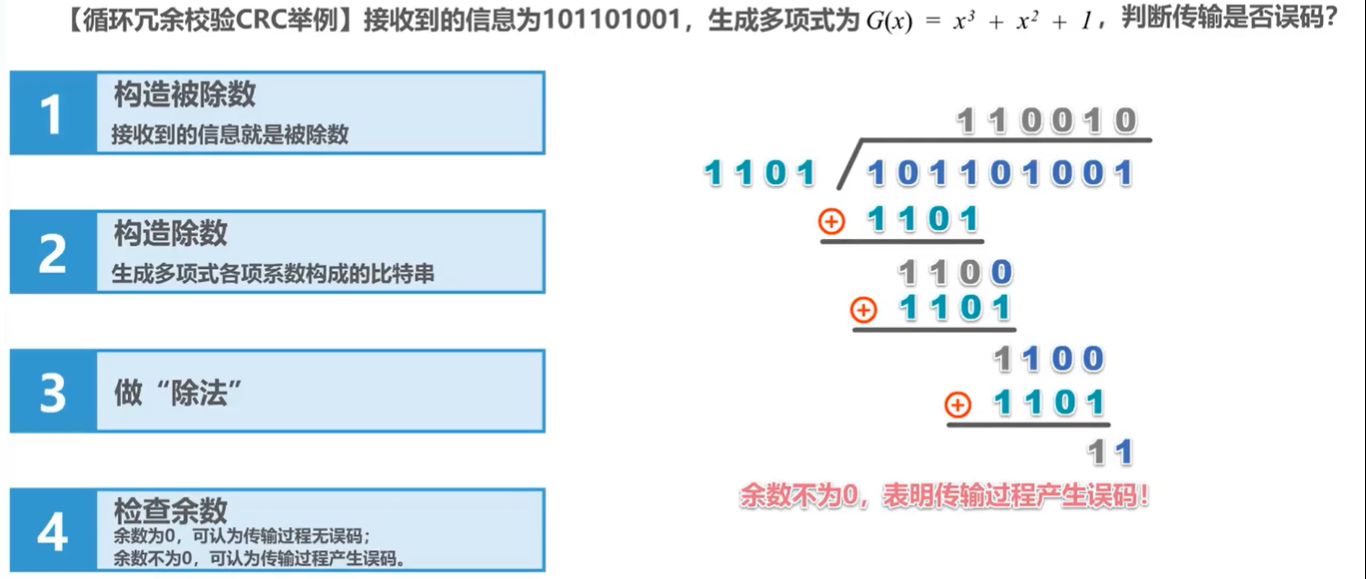 循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确
循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确 -
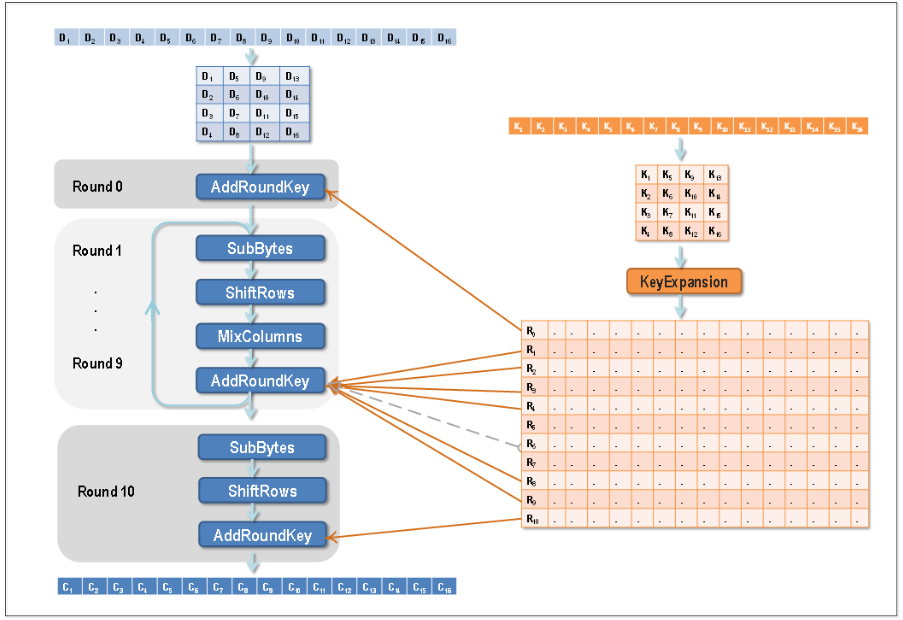 AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛
AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛 -
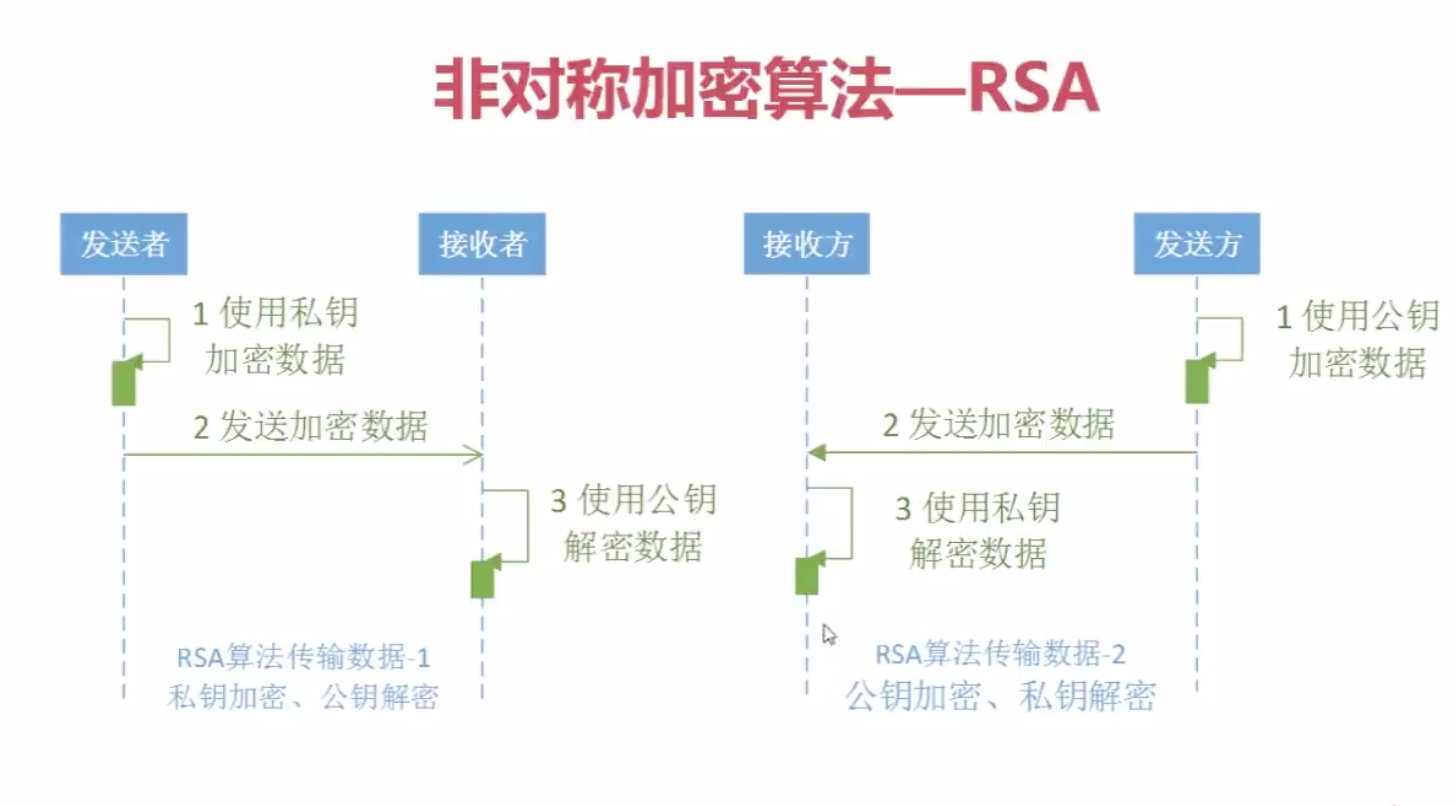 RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难
RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难 -
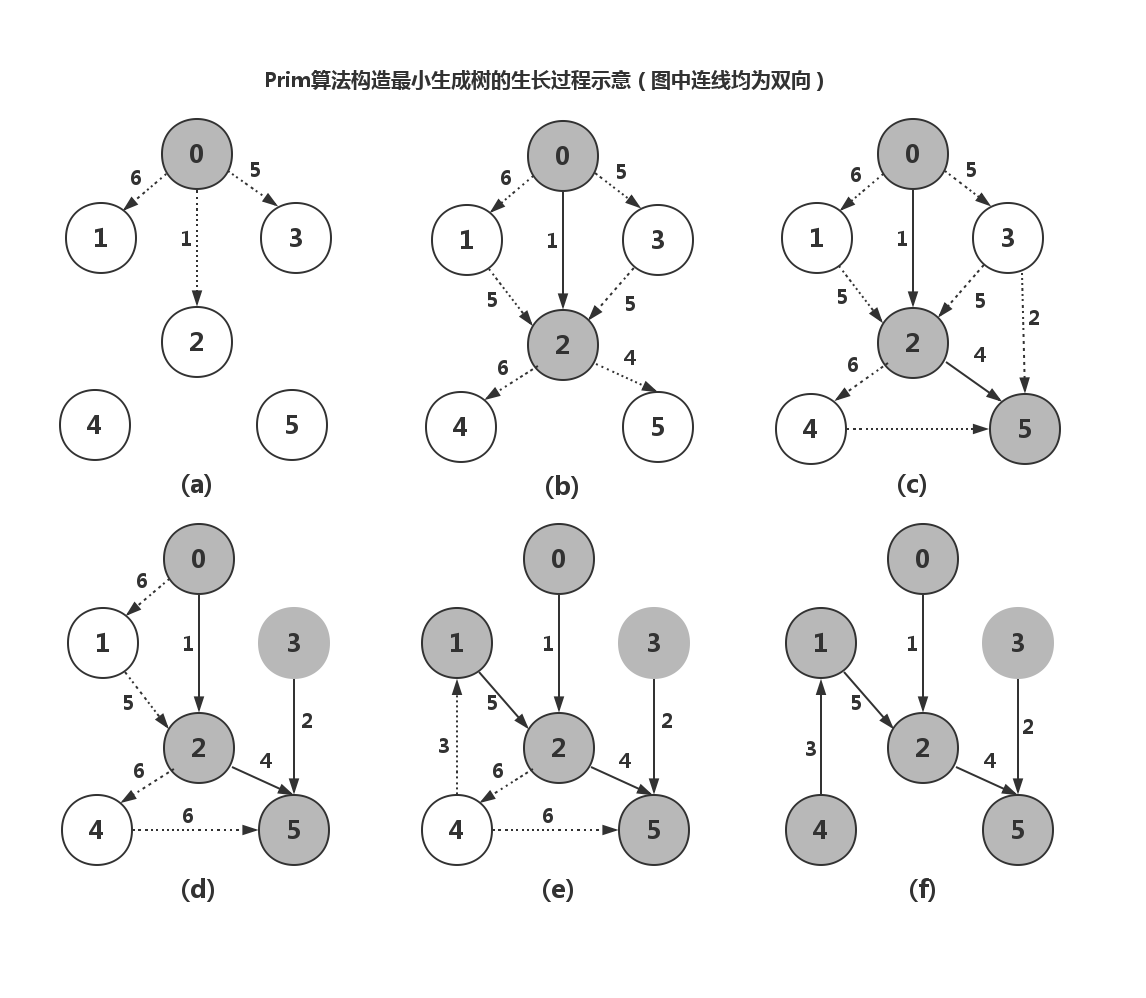 最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添
最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添 -
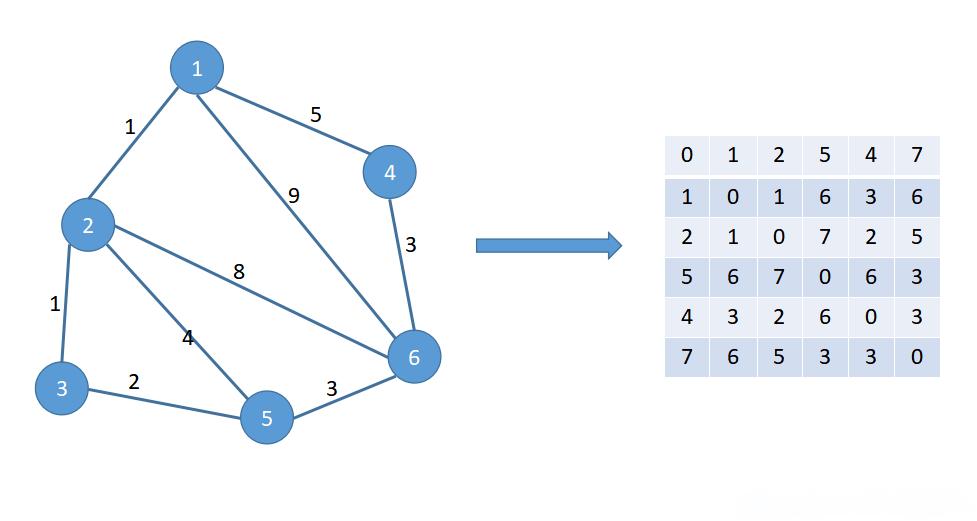 关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选
关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选

