CRC循环冗余校验(Cyclic Redundancy Check,CRC)
循环冗余校验(Cyclic Redundancy Check,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(Error Detection Coding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确认数据在传输过程中是否发生了改变。
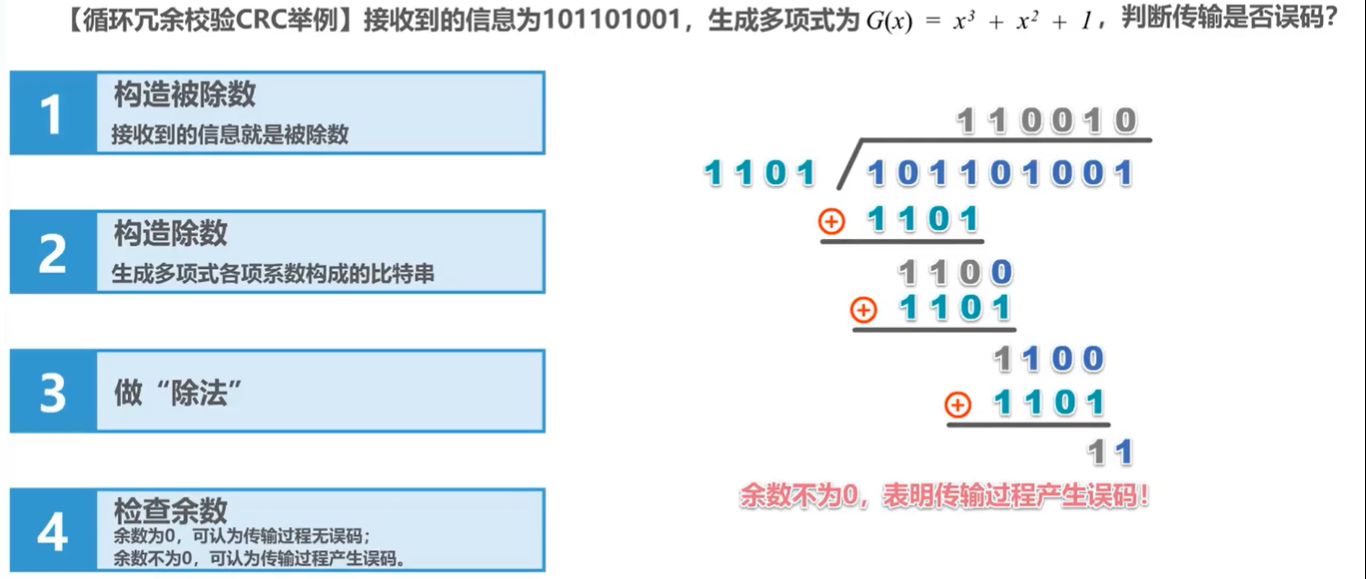
在CRC算法中,原始数据被视为一个二进制多项式,然后用一个预设的生成多项式进行模2除法(也就是异或操作取代了传统的加减乘除),得到的余数就是校验码。在传输过程中,发送方将校验码附加在原始数据尾部一同发送出去;接收方收到数据后,剥离校验码并对剩下的数据重新进行CRC计算,如果计算结果是全0,则认为数据在传输过程中没有发生错误,否则就表示有错误发生。
在具体实现中,CRC常常用于网络通信、磁盘存储、嵌入式系统等领域,确保数据的完整性和一致性。CRC算法有许多变种,主要区别在于所使用的生成多项式的不同,不同的生成多项式会决定CRC校验码的长度和错误检测能力。
在Java中实现CRC校验,你可以使用java.util.zip.CRC32类,它是Java标准库自带的实现,可以方便地计算CRC32校验和。以下是一个使用CRC32进行计算的简单示例:
import java.util.zip.CRC32;
public class CRCExample {
public static void main(String[] args) {
String input = "Hello, World!";
byte[] bytes = input.getBytes();
// 创建一个CRC32实例
CRC32 crc32 = new CRC32();
// 更新CRC值
crc32.update(bytes, 0, bytes.length);
// 获取计算后的CRC值
long crc = crc32.getValue();
// 输出CRC值
System.out.printf("CRC-32 Value for '%s': %d%n", input, crc);
}
}这段代码首先将输入字符串转化为字节数组,然后使用CRC32对象逐步累加字节,最后获取计算好的CRC32校验和。
如果你想实现其他版本的CRC算法,例如CRC16或其他定制的CRC规范,你可能需要手动编写算法或使用第三方库。以下是一个简单的CRC16示例,使用了一个自定义的CRC16计算类:
public class CRC16Example {
// CRC16多项式
private static final int POLYNOMIAL = 0xA001;
// 初始化CRC值
private static final int INITIAL_REMAINDER = 0xFFFF;
public static short calculateCRC16(byte[] bytes) {
short remainder = INITIAL_REMAINDER;
for (byte b : bytes) {
for (int bit = 0x80; bit > 0; bit >>= 1) {
boolean bitIsSet = ((b & bit) > 0);
if ((remainder & 0x0001) == 1) {
remainder >>= 1;
remainder ^= POLYNOMIAL;
} else {
remainder >>= 1;
}
if (bitIsSet) {
remainder ^= POLYNOMIAL;
}
}
}
return remainder;
}
public static void main(String[] args) {
String input = "Hello, World!";
byte[] bytes = input.getBytes();
short crc16 = calculateCRC16(bytes);
System.out.printf("CRC-16 Value for '%s': %04X%n", input, crc16);
}
}以上calculateCRC16方法是一个简单的CRC16算法实现,它不使用表格驱动法或其他优化方法,因此在大数据量下效率较低。实际开发中,你可能需要根据具体CRC规范和性能需求选择合适的方法或库。
原文链接: https://www.yukx.com/arithmetic/article/details/2482.html 优科学习网CRC循环冗余校验(Cyclic Redundancy Check,CRC)
-
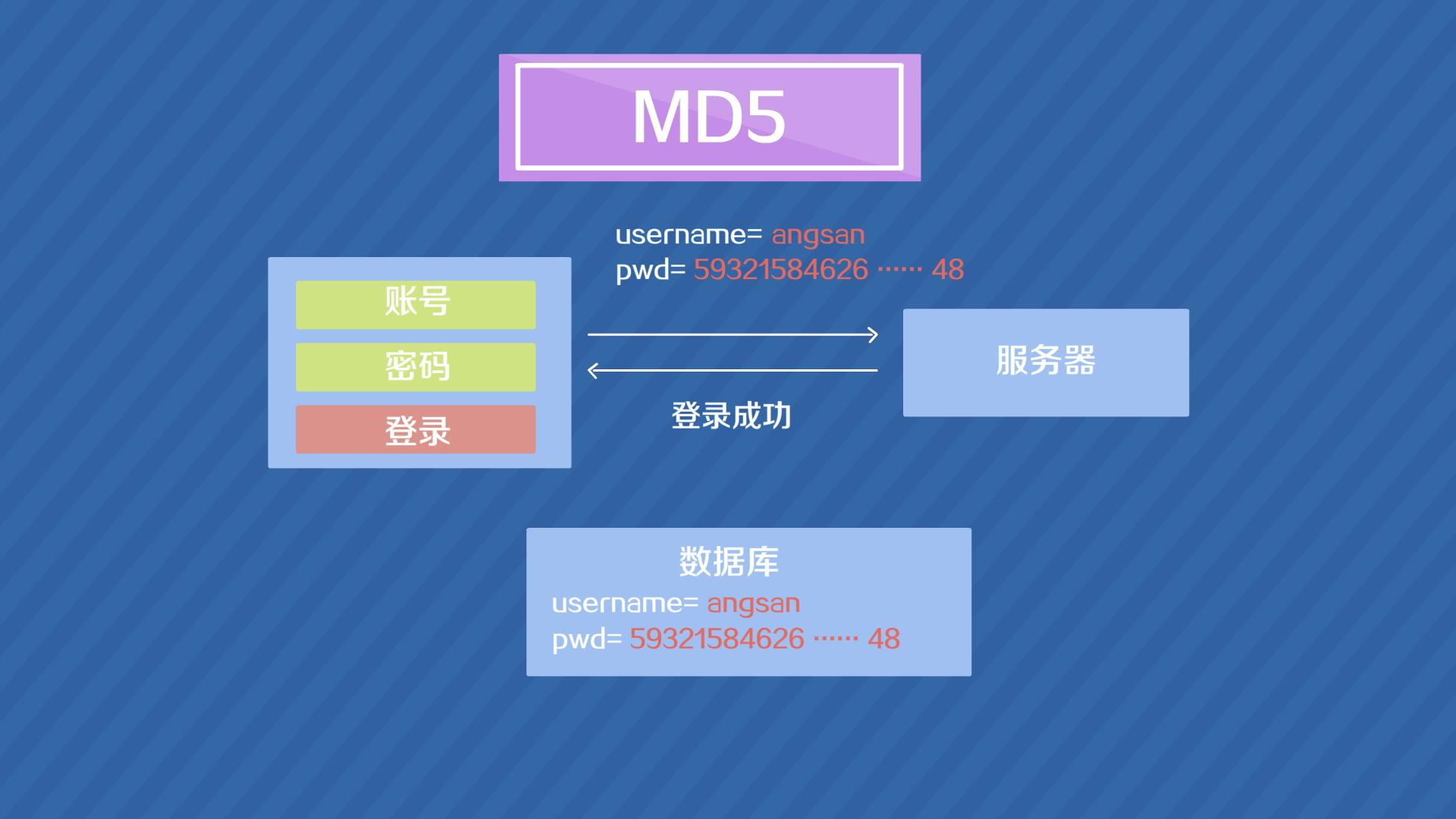 MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到
MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到 -
 循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确
循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确 -
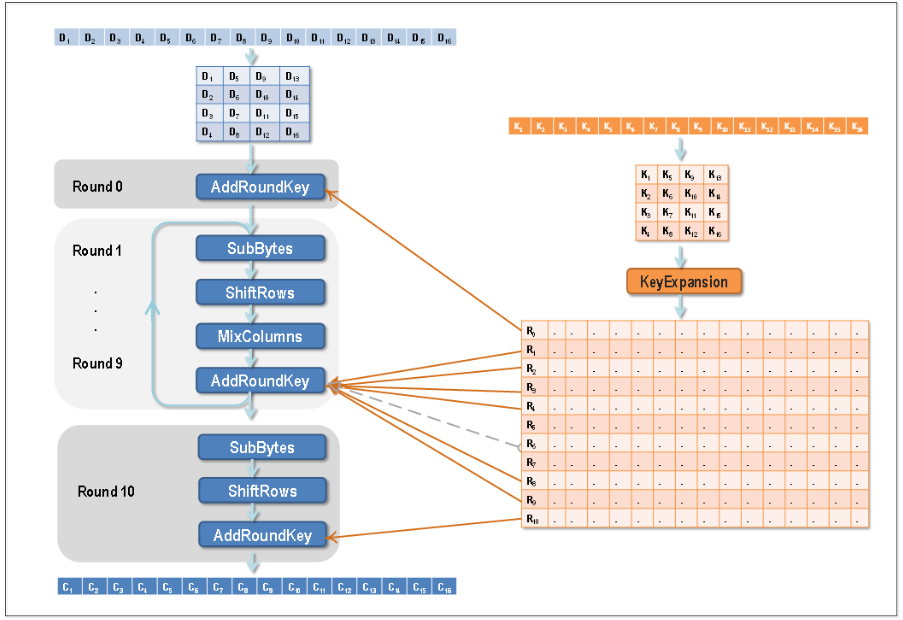 AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛
AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛 -
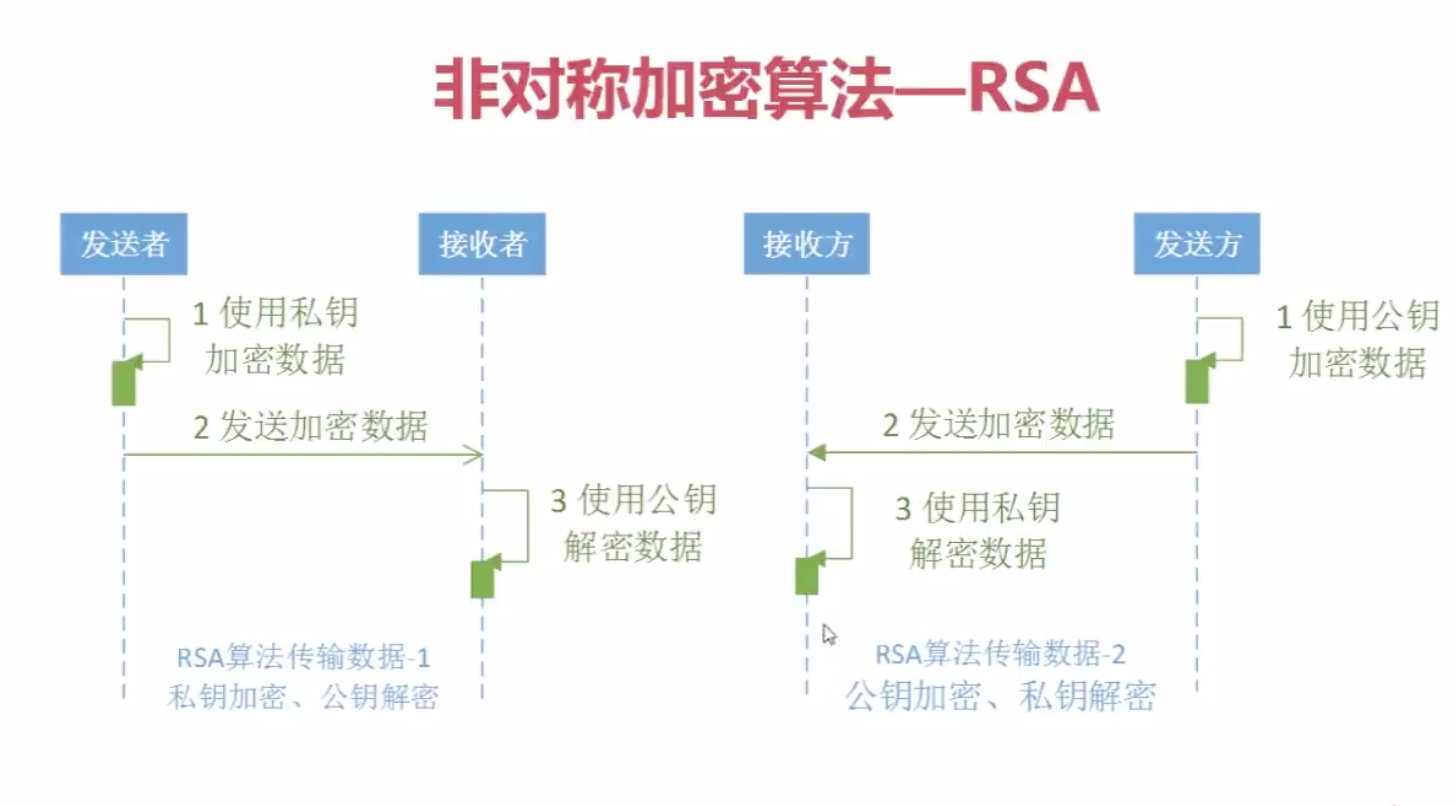 RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难
RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难 -
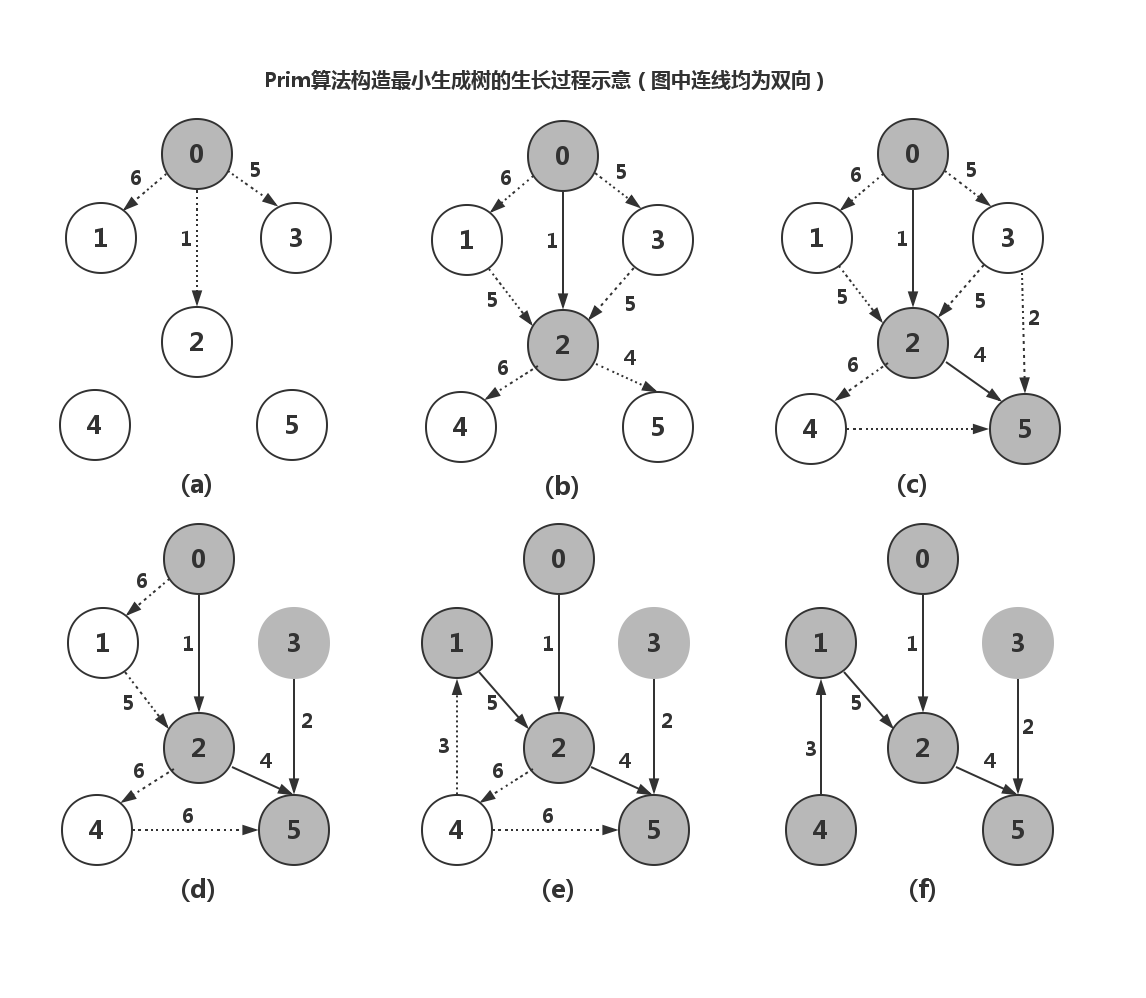 最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添
最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添 -
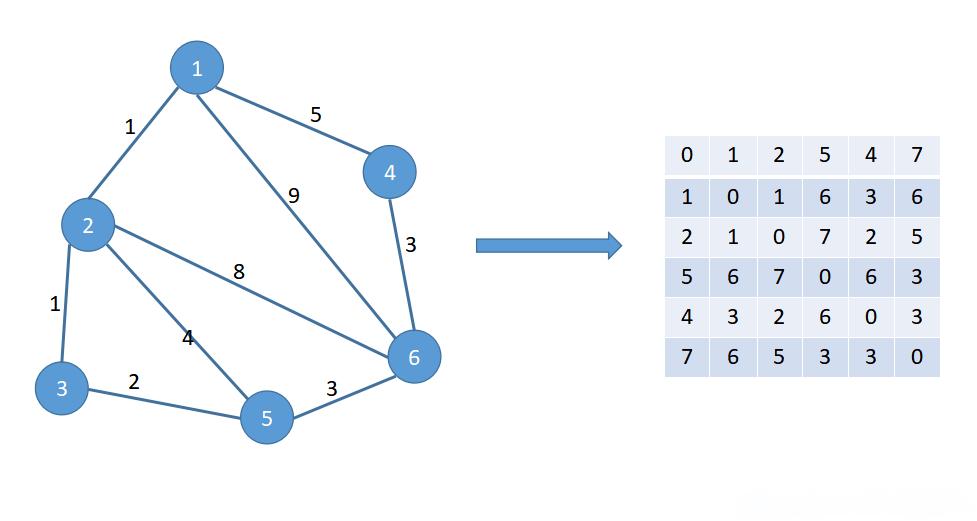 关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选
关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选

