SparkRDD操作
Spark RDD 操作
RDDs 支持 2 种类型的操作:转换(transformations) 从已经存在的数据集中创建一个新的数据集;动作(actions) 在数据集上进行计算之后返回一个值到驱动程序。例如,map 是一个转换操作,它将每一个数据集元素传递给一个函数并且返回一个新的 RDD。另一方面,reduce 是一个动作,它使用相同的函数来聚合 RDD 的所有元素,并且将最终的结果返回到驱动程序(不过也有一个并行 reduceByKey 能返回一个分布式数据集)。
在 Spark 中,所有的转换(transformations)都是惰性(lazy)的,它们不会马上计算它们的结果。相反的,它们仅仅记录转换操作是应用到哪些基础数据集(例如一个文件)上的。转换仅仅在这个时候计算:当动作(action) 需要一个结果返回给驱动程序的时候。这个设计能够让 Spark 运行得更加高效。例如,我们可以实现:通过 map 创建一个新数据集在 reduce 中使用,并且仅仅返回 reduce 的结果给 driver,而不是整个大的映射过的数据集。
默认情况下,每一个转换过的 RDD 会在每次执行动作(action)的时候重新计算一次。然而,你也可以使用 persist (或 cache)方法持久化(persist)一个 RDD 到内存中。在这个情况下,Spark 会在集群上保存相关的元素,在你下次查询的时候会变得更快。在这里也同样支持持久化 RDD 到磁盘,或在多个节点间复制。
基础
为了说明 RDD 基本知识,考虑下面的简单程序:
val lines = sc.textFile("data.txt")
val lineLengths = lines.map(s => s.length)
val totalLength = lineLengths.reduce((a, b) => a + b)第一行是定义来自于外部文件的 RDD。这个数据集并没有加载到内存或做其他的操作:lines 仅仅是一个指向文件的指针。第二行是定义 lineLengths,它是 map 转换(transformation)的结果。同样,lineLengths 由于懒惰模式也没有立即计算。最后,我们执行 reduce,它是一个动作(action)。在这个地方,Spark 把计算分成多个任务(task),并且让它们运行在多个机器上。每台机器都运行自己的 map 部分和本地 reduce 部分。然后仅仅将结果返回给驱动程序。
如果我们想要再次使用 lineLengths,我们可以添加:
lineLengths.persist()在 reduce 之前,它会导致 lineLengths 在第一次计算完成之后保存到内存中。
原文链接: https://www.yukx.com/bigdata/article/details/825.html 优科学习网SparkRDD操作
-
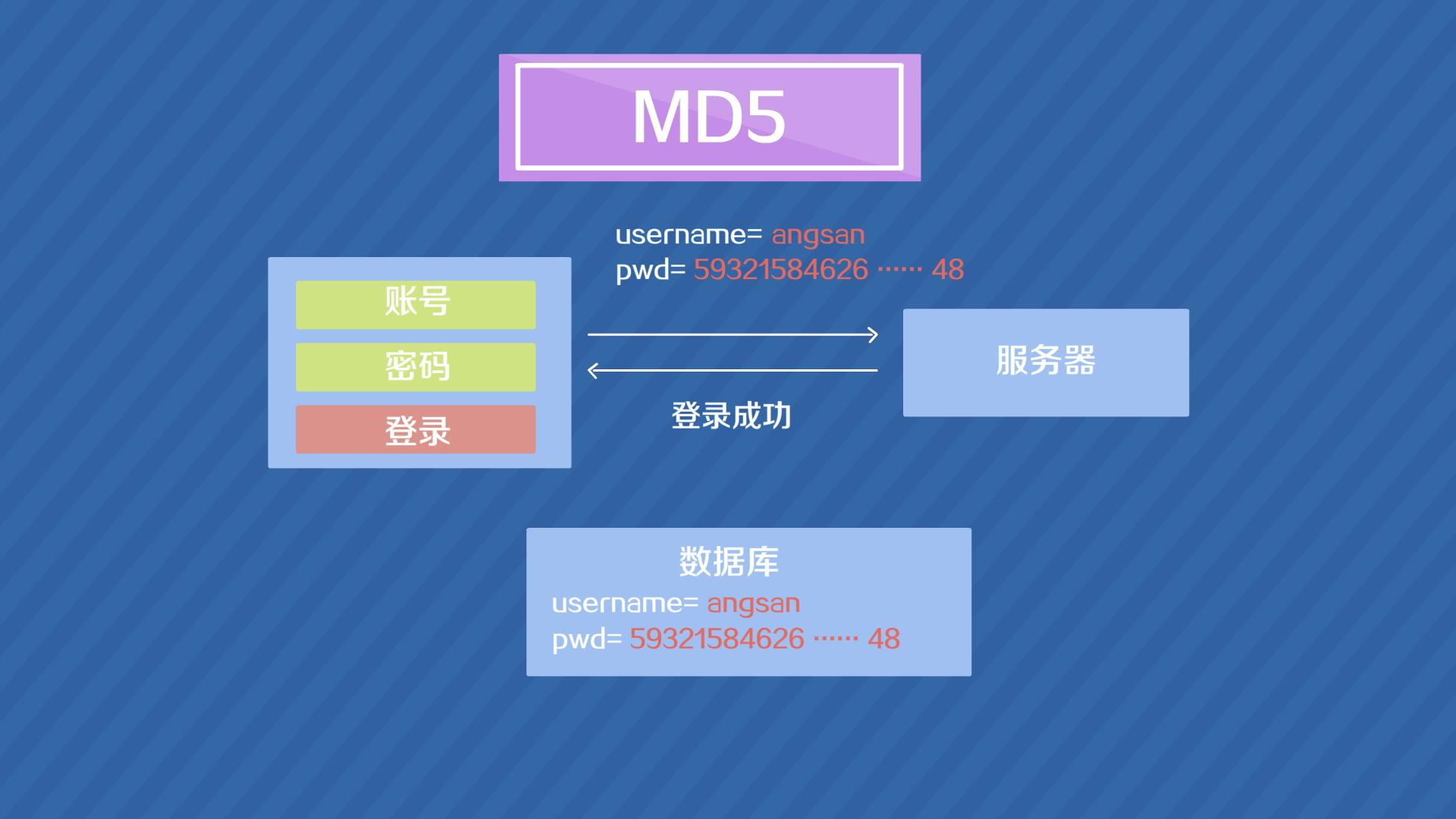 MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到
MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到 -
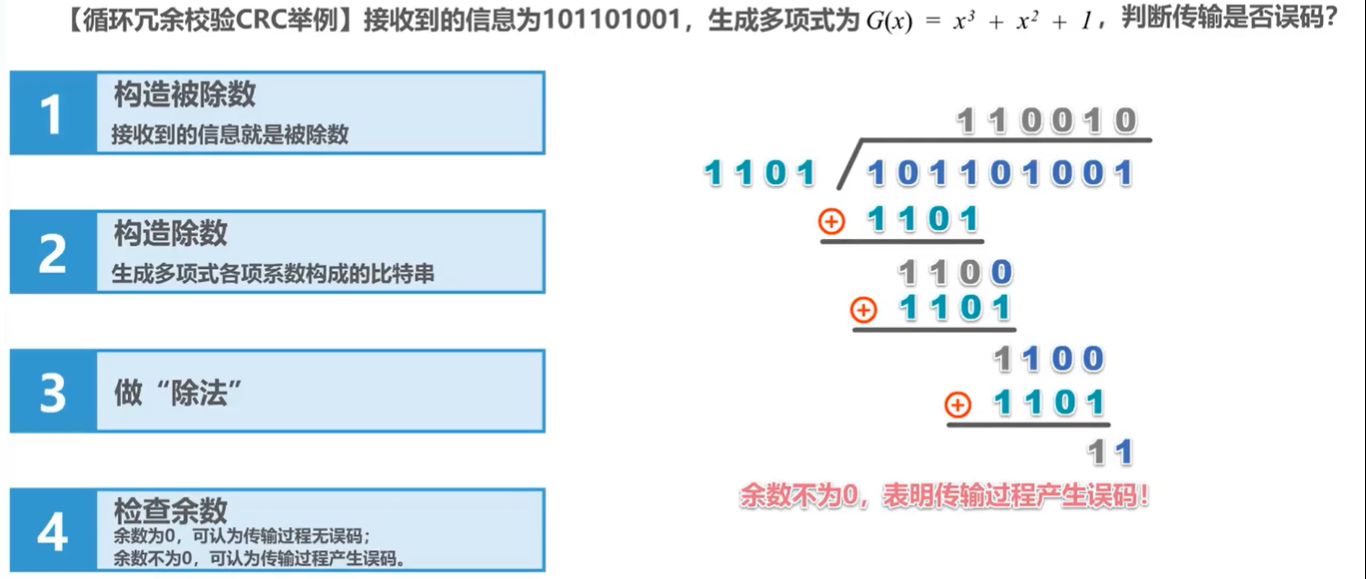 循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确
循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确 -
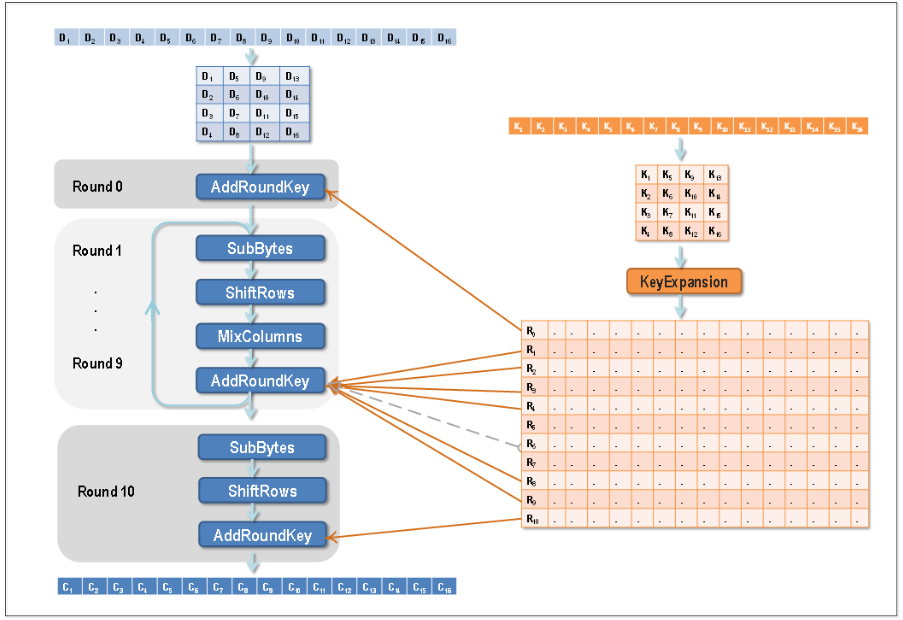 AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛
AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛 -
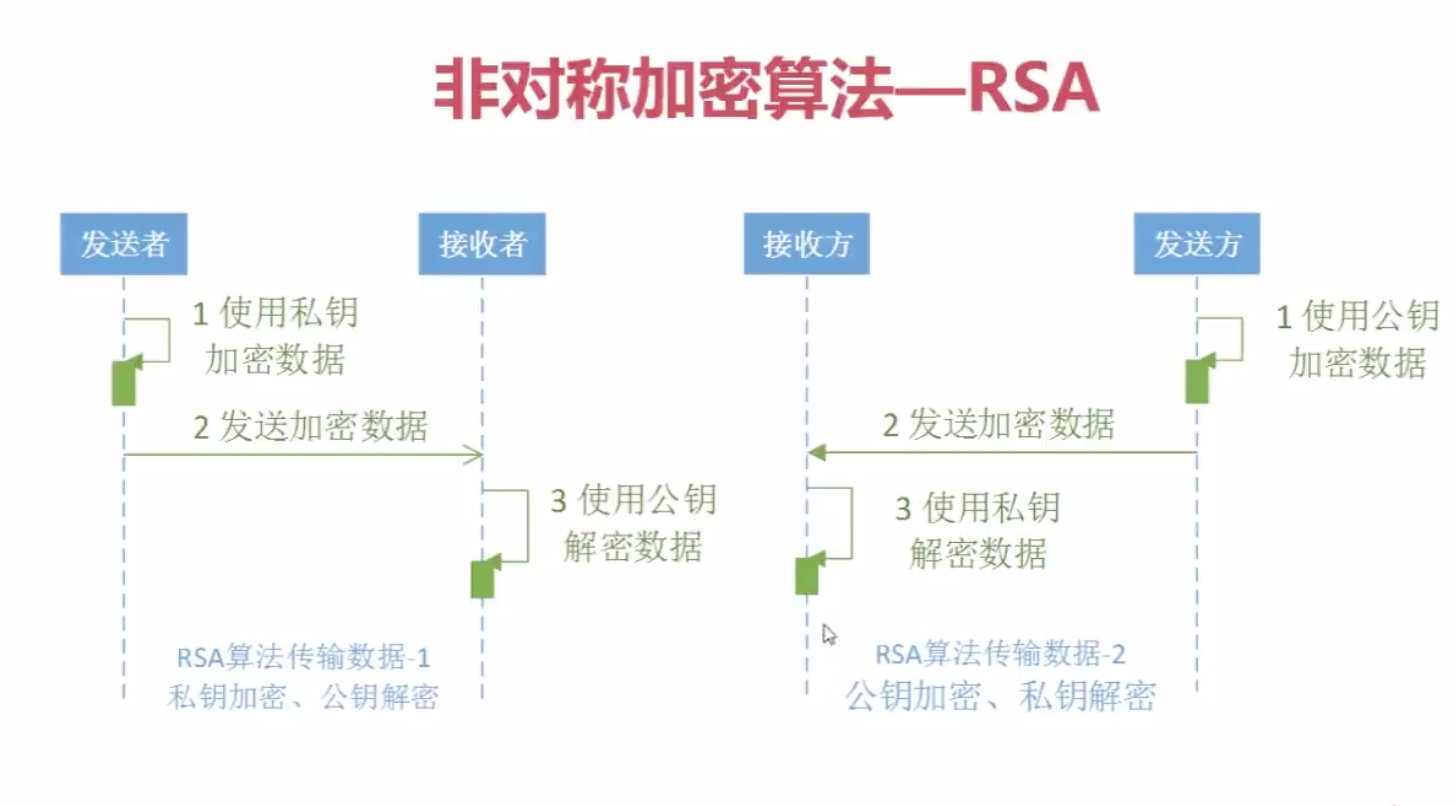 RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难
RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难 -
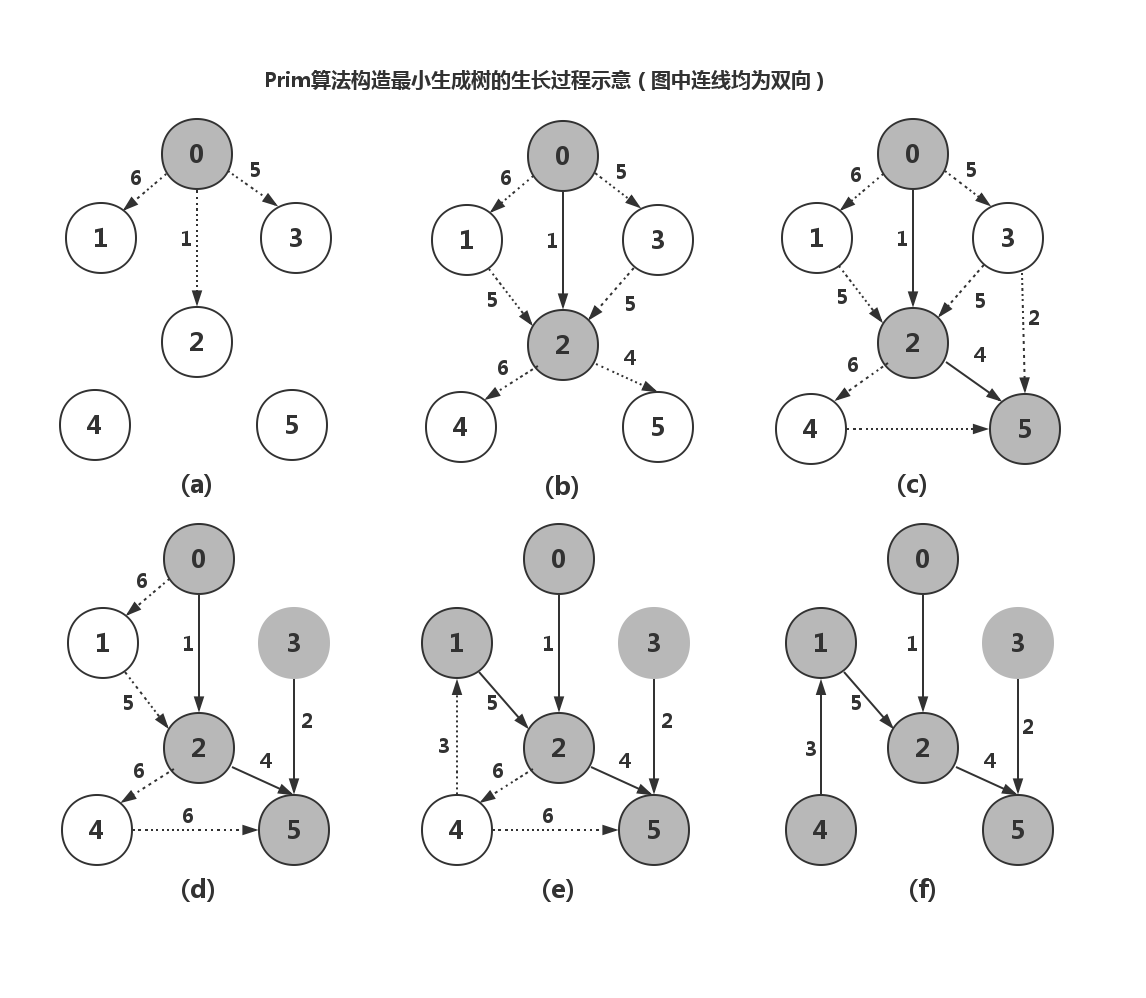 最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添
最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添 -
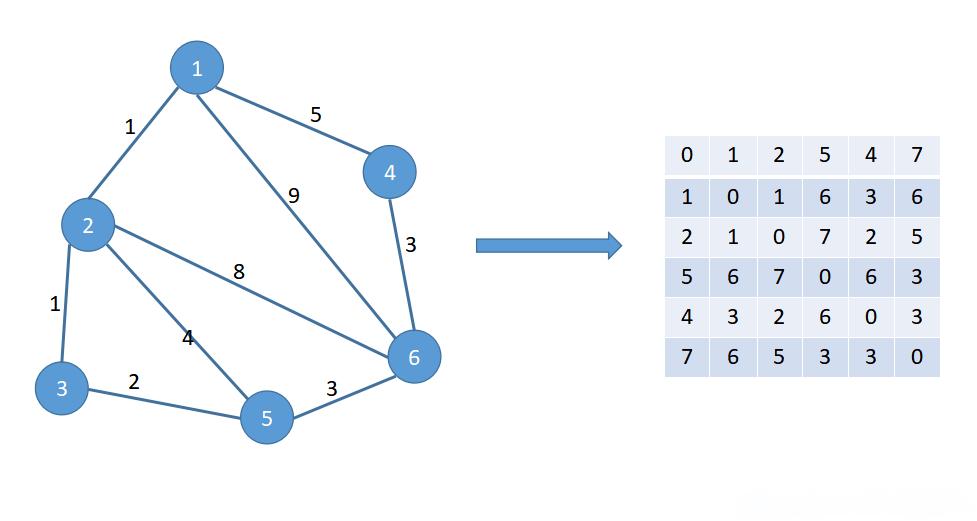 关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选
关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选

