SparkGraphX顶点和边RDDs
Spark GraphX顶点和边RDDs
GraphX暴露保存在图中的顶点和边的RDD。然而,因为GraphX包含的顶点和边拥有优化的数据结构,这些数据结构提供了额外的功能。顶点和边分别返回VertexRDD和EdgeRDD。这一章我们将学习它们的一些有用的功能。
VertexRDDs
VertexRDD[A]继承自RDD[(VertexID, A)]并且添加了额外的限制,那就是每个VertexID只能出现一次。此外,VertexRDD[A]代表了一组属性类型为A的顶点。在内部,这通过保存顶点属性到一个可重复使用的hash-map数据结构来获得。所以,如果两个VertexRDDs从相同的基本VertexRDD获得(如通过filter或者mapValues),它们能够在固定的时间内连接而不需要hash评价。为了利用这个索引数据结构,VertexRDD暴露了一下附加的功能:
class VertexRDD[VD] extends RDD[(VertexID, VD)] {
// Filter the vertex set but preserves the internal index
def filter(pred: Tuple2[VertexId, VD] => Boolean): VertexRDD[VD]
// Transform the values without changing the ids (preserves the internal index)
def mapValues[VD2](map: VD => VD2): VertexRDD[VD2]
def mapValues[VD2](map: (VertexId, VD) => VD2): VertexRDD[VD2]
// Remove vertices from this set that appear in the other set
def diff(other: VertexRDD[VD]): VertexRDD[VD]
// Join operators that take advantage of the internal indexing to accelerate joins (substantially)
def leftJoin[VD2, VD3](other: RDD[(VertexId, VD2)])(f: (VertexId, VD, Option[VD2]) => VD3): VertexRDD[VD3]
def innerJoin[U, VD2](other: RDD[(VertexId, U)])(f: (VertexId, VD, U) => VD2): VertexRDD[VD2]
// Use the index on this RDD to accelerate a `reduceByKey` operation on the input RDD.
def aggregateUsingIndex[VD2](other: RDD[(VertexId, VD2)], reduceFunc: (VD2, VD2) => VD2): VertexRDD[VD2]
}举个例子,filter操作如何返回一个VertexRDD。过滤器实际使用一个BitSet实现,因此它能够重用索引以及保留和其它VertexRDDs做连接时速度快的能力。同样的,mapValues操作不允许map函数改变VertexID,因此可以保证相同的HashMap数据结构能够重用。当连接两个从相同的hashmap获取的VertexRDDs和使用线性扫描而不是昂贵的点查找实现连接操作时,leftJoin和innerJoin都能够使用。
从一个RDD[(VertexID, A)]高效地构建一个新的VertexRDD,aggregateUsingIndex操作是有用的。概念上,如果我通过一组顶点构造了一个VertexRDD[B],而VertexRDD[B]是一些RDD[(VertexID, A)]中顶点的超集,那么我们就可以在聚合以及随后索引RDD[(VertexID, A)]中重用索引。例如:
val setA: VertexRDD[Int] = VertexRDD(sc.parallelize(0L until 100L).map(id => (id, 1)))
val rddB: RDD[(VertexId, Double)] = sc.parallelize(0L until 100L).flatMap(id => List((id, 1.0), (id, 2.0)))
// There should be 200 entries in rddB
rddB.count
val setB: VertexRDD[Double] = setA.aggregateUsingIndex(rddB, _ + _)
// There should be 100 entries in setB
setB.count
// Joining A and B should now be fast!
val setC: VertexRDD[Double] = setA.innerJoin(setB)((id, a, b) => a + b)EdgeRDDs
EdgeRDD[ED]继承自RDD[Edge[ED]],使用定义在PartitionStrategy的各种分区策略中的一个在块分区中组织边。在每个分区中,边属性和相邻结构被分别保存,当属性值改变时,它们可以最大化的重用。
EdgeRDD暴露了三个额外的函数
// Transform the edge attributes while preserving the structure
def mapValues[ED2](f: Edge[ED] => ED2): EdgeRDD[ED2]
// Revere the edges reusing both attributes and structure
def reverse: EdgeRDD[ED]
// Join two `EdgeRDD`s partitioned using the same partitioning strategy.
def innerJoin[ED2, ED3](other: EdgeRDD[ED2])(f: (VertexId, VertexId, ED, ED2) => ED3): EdgeRDD[ED3]在大多数的应用中,我们发现,EdgeRDD操作可以通过图操作者(graph operators)或者定义在基本RDD中的操作来完成。
原文链接: https://www.yukx.com/bigdata/article/details/862.html 优科学习网SparkGraphX顶点和边RDDs
-
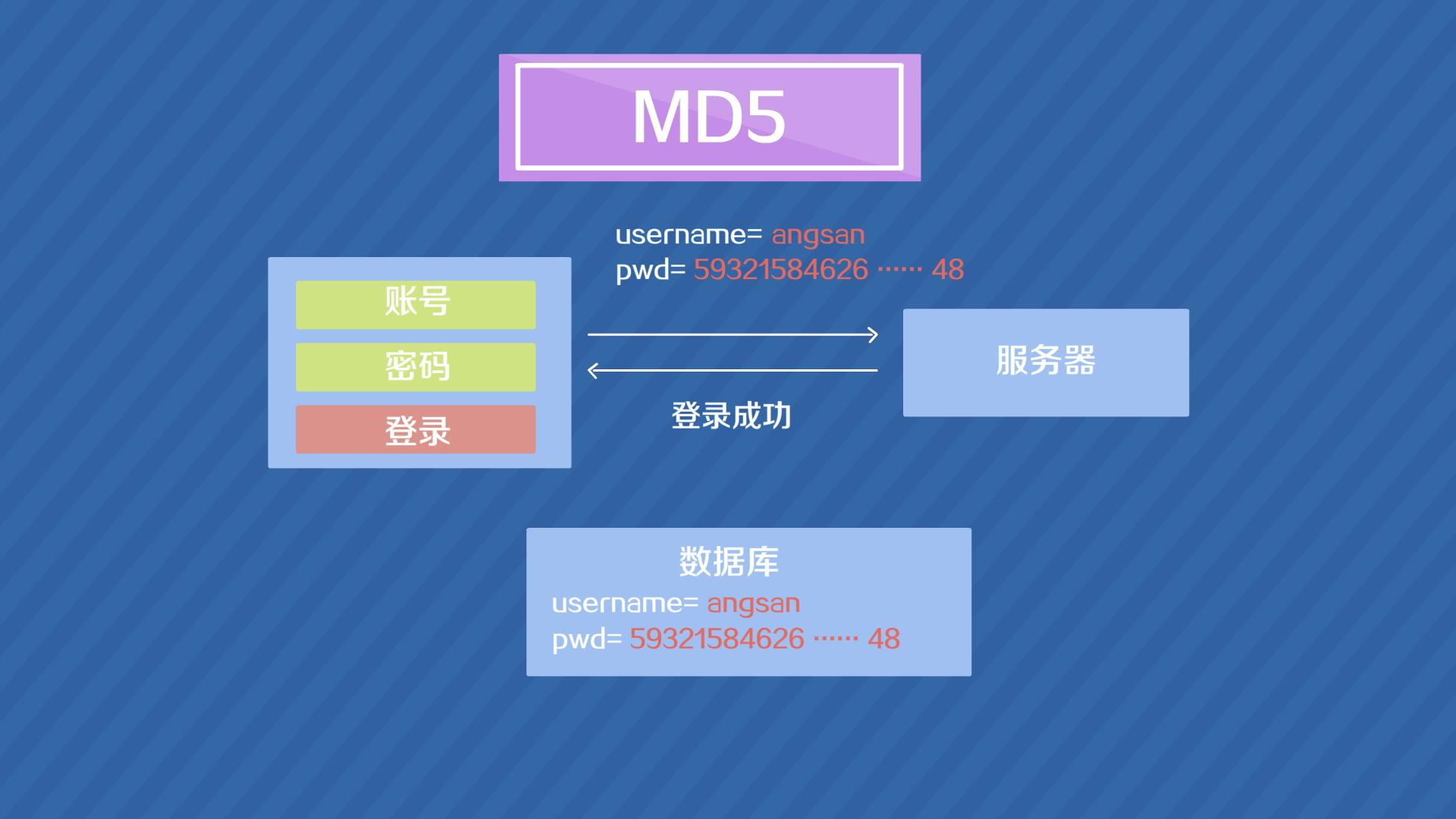 MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到
MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到 -
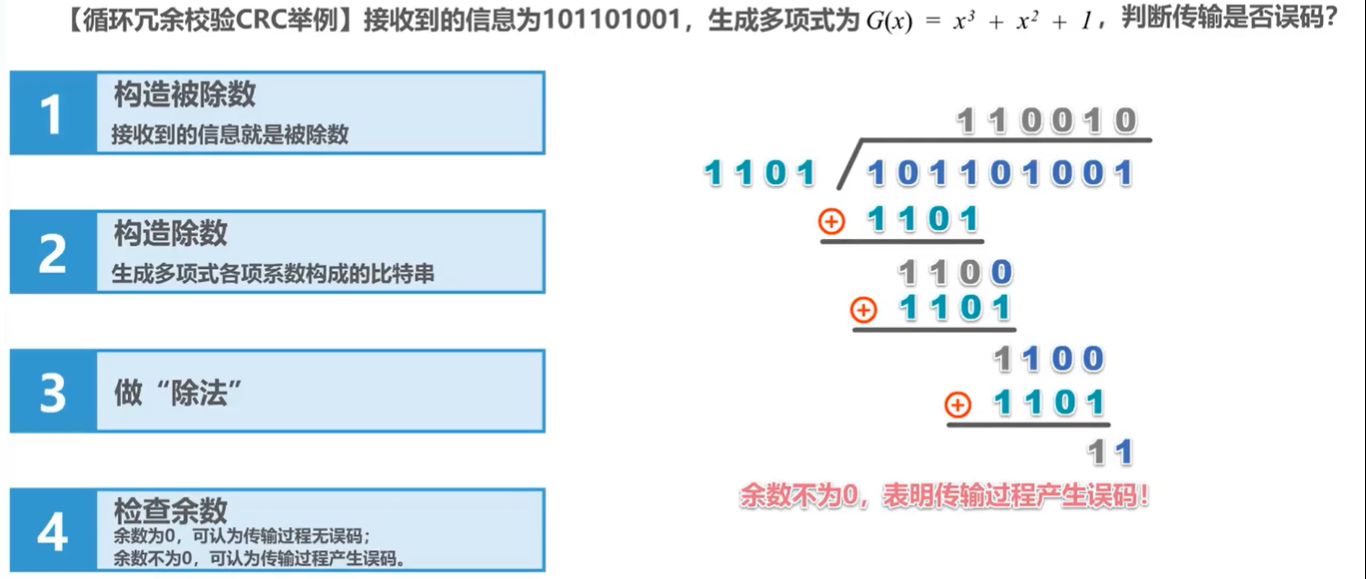 循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确
循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确 -
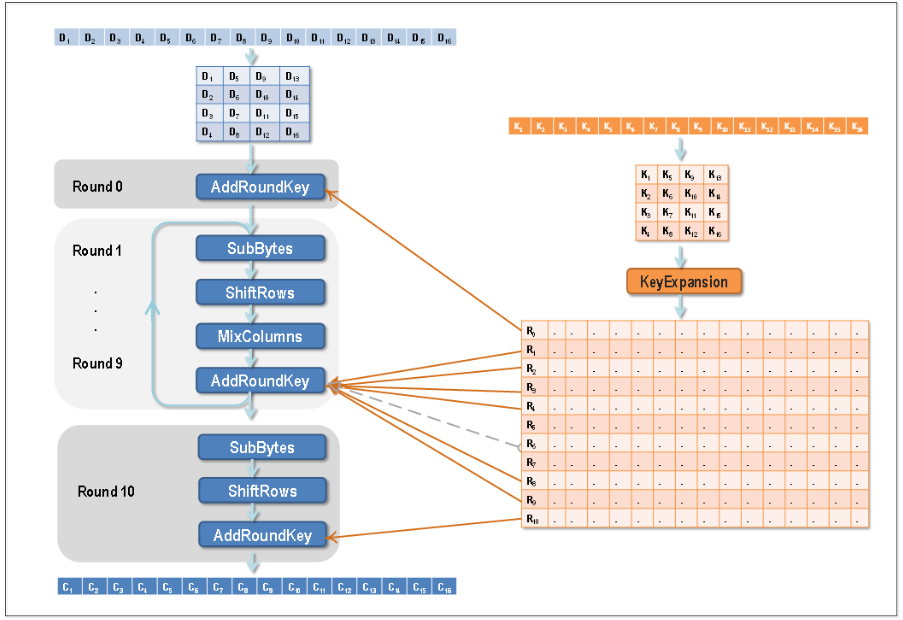 AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛
AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛 -
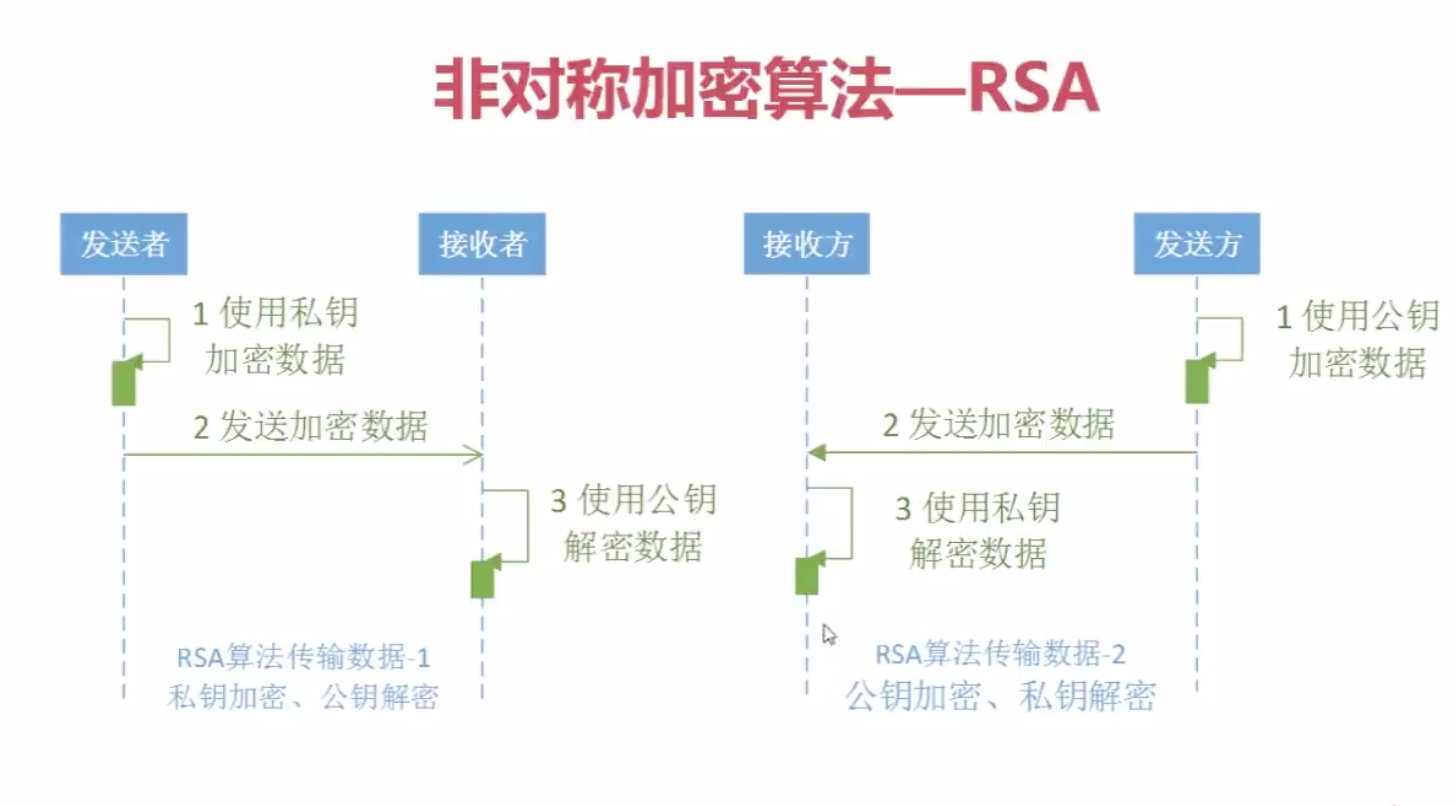 RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难
RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难 -
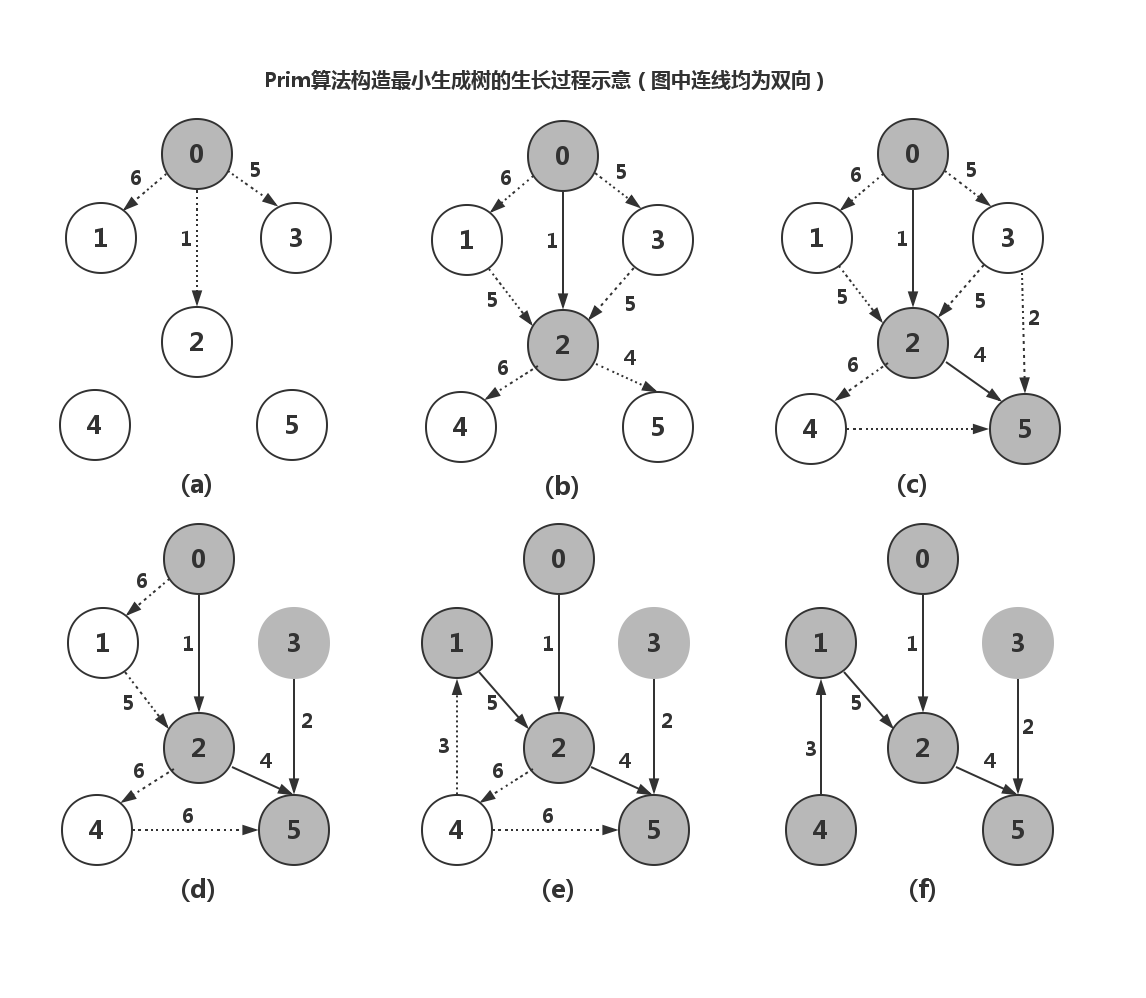 最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添
最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添 -
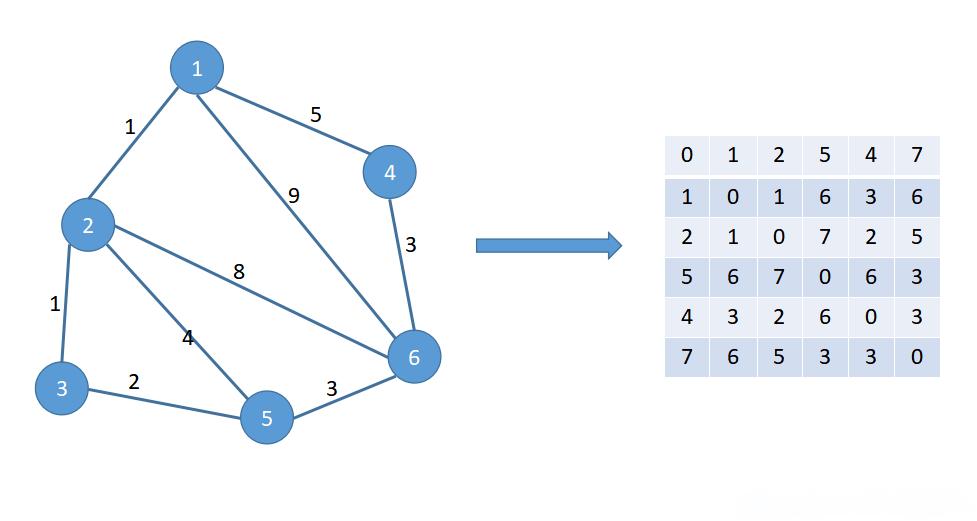 关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选
关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选

