SparkGraphX属性图
Spark GraphX属性图
属性图是一个有向多重图,它带有连接到每个顶点和边的用户定义的对象。有向多重图中多个并行(parallel)的边共享相同的源和目的地顶点。支持并行边的能力简化了建模场景,这个场景中,相同的顶点存在多种关系(例如co-worker和friend)。每个顶点由一个唯一的64位长的标识符(VertexID)作为key。GraphX并没有对顶点标识强加任何排序。同样,顶点拥有相应的源和目的顶点标识符。
属性图通过vertex(VD)和edge(ED)类型参数化,这些类型是分别与每个顶点和边相关联的对象的类型。
在某些情况下,在相同的图形中,可能希望顶点拥有不一样的属性类型。这可以通过继承完成。例如,将用户和产品建模成一个二分图,我们可以用如下方式
class VertexProperty()
case class UserProperty(val name: String) extends VertexProperty
case class ProductProperty(val name: String, val price: Double) extends VertexProperty
// The graph might then have the type:
var graph: Graph[VertexProperty, String] = null和RDD一样,属性图是不可变的、分布式的、容错的。图的值或者结构的改变需要按期望的生成一个新的图来实现。注意,原始图的大部分都可以在新图中重用,用来减少这种固有的功能数据结构的成本。执行者使用一系列顶点分区试探法来对图进行分区。如RDD一样,图中的每个分区可以在发生故障的情况下被重新创建在不一样的机器上。
逻辑上的属性图对应于一对类型化的集合(RDD),这个集合编码了每一个顶点和边的属性。因此,图类包含访问图中顶点和边的成员。
class Graph[VD, ED] {
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
}VertexRDD[VD]和EdgeRDD[ED]类分别继承和优化自RDD[(VertexID, VD)]和RDD[Edge[ED]]。VertexRDD[VD]和EdgeRDD[ED]都支持额外的功能来建立在图计算和利用内部优化。
属性图的例子
在GraphX项目中,假设我们想构造一个包括不一样合作者的属性图。顶点属性可能包含用户名和职业。我们可以用描述合作者之间关系的字符串标注边缘。

所得的图形将具有类型签名
val userGraph: Graph[(String, String), String]有很多方式从一个原始文件、RDD构造一个属性图。最通常的方法是利用Graph object。下面的代码从RDD集合生成属性图。
// Assume the SparkContext has already been constructed
val sc: SparkContext
// Create an RDD for the vertices
val users: RDD[(VertexId, (String, String))] =
sc.parallelize(Array((3L, ("rxin", "student")), (7L, ("jgonzal", "postdoc")),
(5L, ("franklin", "prof")), (2L, ("istoica", "prof"))))
// Create an RDD for edges
val relationships: RDD[Edge[String]] =
sc.parallelize(Array(Edge(3L, 7L, "collab"), Edge(5L, 3L, "advisor"),
Edge(2L, 5L, "colleague"), Edge(5L, 7L, "pi")))
// Define a default user in case there are relationship with missing user
val defaultUser = ("John Doe", "Missing")
// Build the initial Graph
val graph = Graph(users, relationships, defaultUser)在上面的例子中,我们用到了Edge样本类。边有一个srcId和dstId分别对应于源和目标顶点的标示符。另外,Edge类有一个attr成员用来存储边属性。
我们可以分别用graph.vertices和graph.edges成员将一个图解构为相应的顶点和边。
val graph: Graph[(String, String), String] // Constructed from above
// Count all users which are postdocs
graph.vertices.filter { case (id, (name, pos)) => pos == "postdoc" }.count
// Count all the edges where src > dst
graph.edges.filter(e => e.srcId > e.dstId).count注意,graph.vertices返回一个VertexRDD[(String, String)],它继承于 RDD[(VertexID, (String, String))]。所以我们可以用scala的case表达式解构这个元组。另一方面,
graph.edges返回一个包含Edge[String]对象的EdgeRDD。我们也可以用到case类的类型构造器,如下例所示。
graph.edges.filter { case Edge(src, dst, prop) => src > dst }.count除了属性图的顶点和边视图,GraphX也包含了一个三元组视图,三元视图逻辑上将顶点和边的属性保存为一个RDD[EdgeTriplet[VD, ED]],它包含EdgeTriplet类的实例。可以通过下面的Sql表达式表示这个连接。
SELECT src.id, dst.id, src.attr, e.attr, dst.attr
FROM edges AS e LEFT JOIN vertices AS src, vertices AS dst
ON e.srcId = src.Id AND e.dstId = dst.Id或者通过下面的图来表示。

EdgeTriplet类继承于Edge类,并且加入了srcAttr和dstAttr成员,这两个成员分别包含源和目的的属性。我们可以用一个三元组视图渲染字符串集合用来描述用户之间的关系。
val graph: Graph[(String, String), String] // Constructed from above
// Use the triplets view to create an RDD of facts.
val facts: RDD[String] =
graph.triplets.map(triplet =>
triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1)
facts.collect.foreach(println(_))原文链接: https://www.yukx.com/bigdata/article/details/857.html 优科学习网SparkGraphX属性图
-
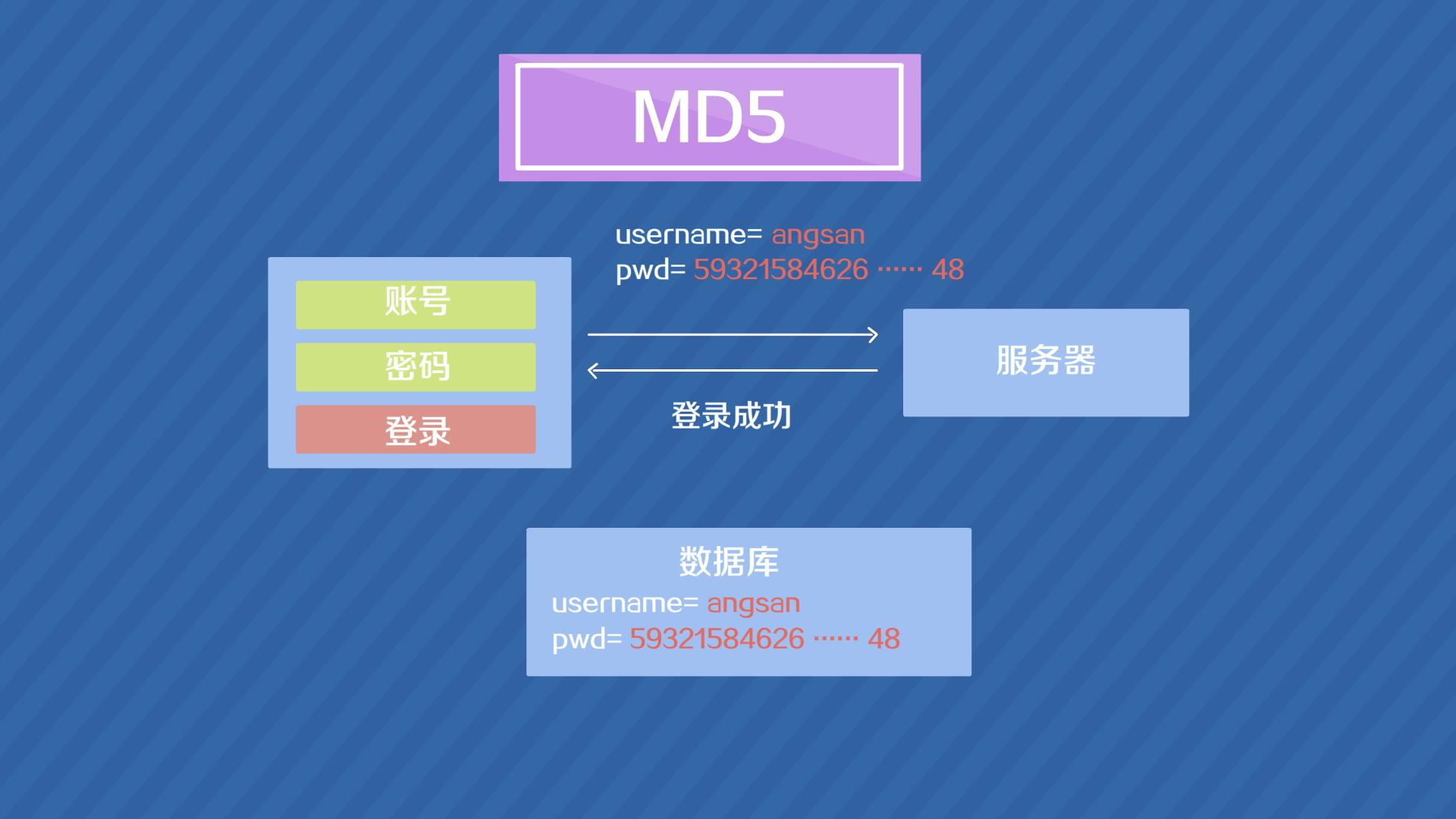 MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到
MD5(Message-DigestAlgorithm5)是一种广泛使用的散列函数(哈希函数),由美国密码学家罗纳德·李维斯特(RonaldL.Rivest)在1991年设计。MD5的作用是对任意长度的信息生成一个固定长度(128位,即32个十六进制字符)的“指纹”或“消息摘要”,并且几乎不可能找到 -
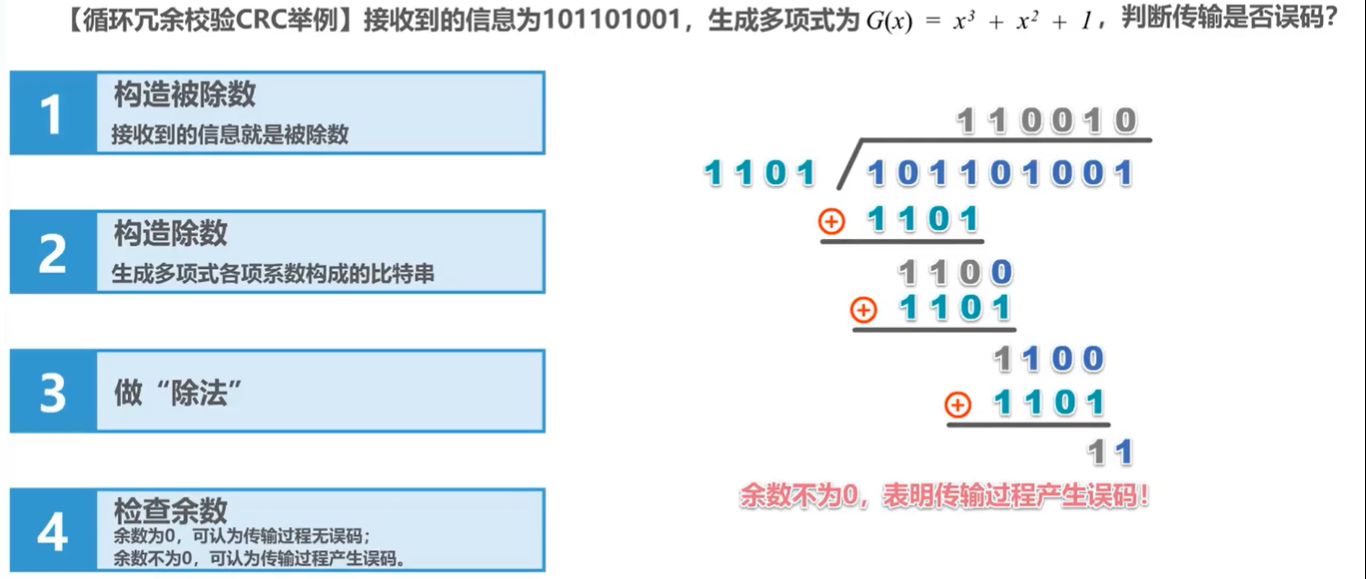 循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确
循环冗余校验(CyclicRedundancyCheck,CRC)是一种用于检测数据传输和存储过程中发生错误的技术,属于一种基于数学原理的错误检测编码(ErrorDetectionCoding)方法。它通过在原始数据上附加一个固定长度的校验码,使得接收端可以通过同样的计算规则对收到的数据进行校验,确 -
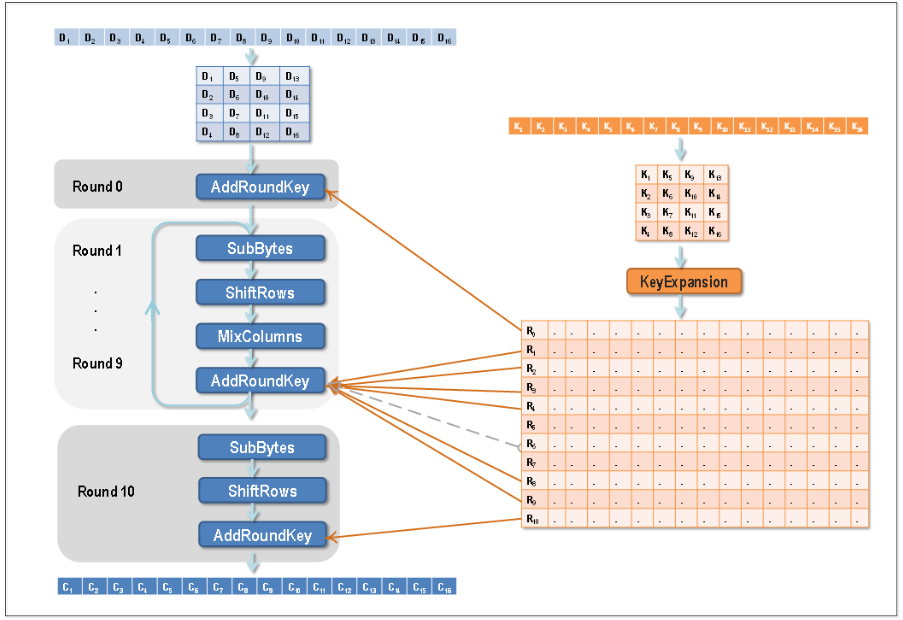 AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛
AES(AdvancedEncryptionStandard)是一种广泛使用的对称密钥加密算法,它是美国国家标准与技术研究院(NIST)于2001年制定的加密标准,用于替代原有的DES(DataEncryptionStandard)。AES算法以其高效性、安全性和可靠性而著称,在众多应用领域中被广泛 -
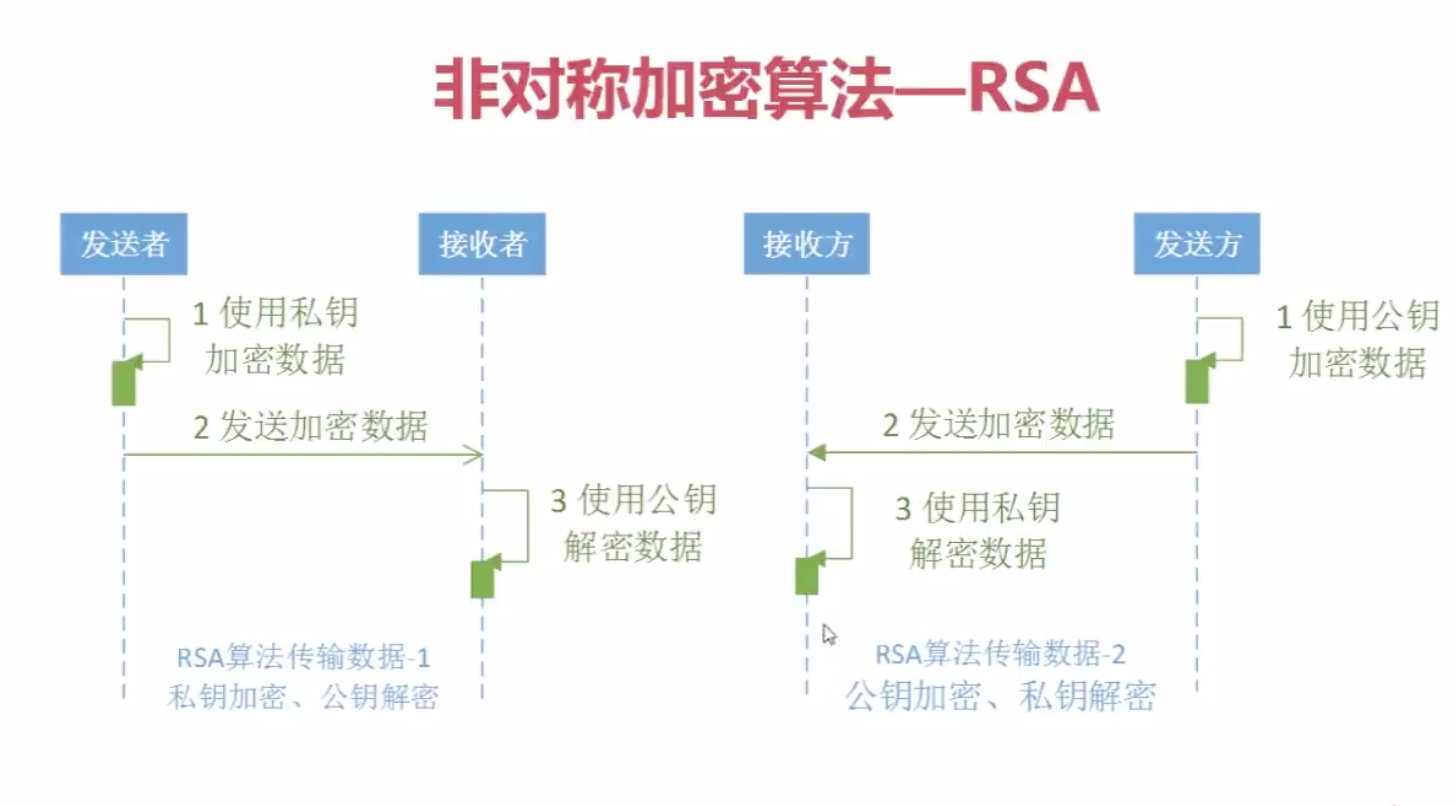 RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难
RSA(Rivest-Shamir-Adleman)是一种广泛应用的非对称加密算法,由RonRivest、AdiShamir和LenAdleman在1977年提出。其安全性基于数学上的大数因子分解难题,即对于足够大的两个素数p和q而言,已知它们的乘积很容易,但想要从这个乘积中恢复原始的素数则异常困难 -
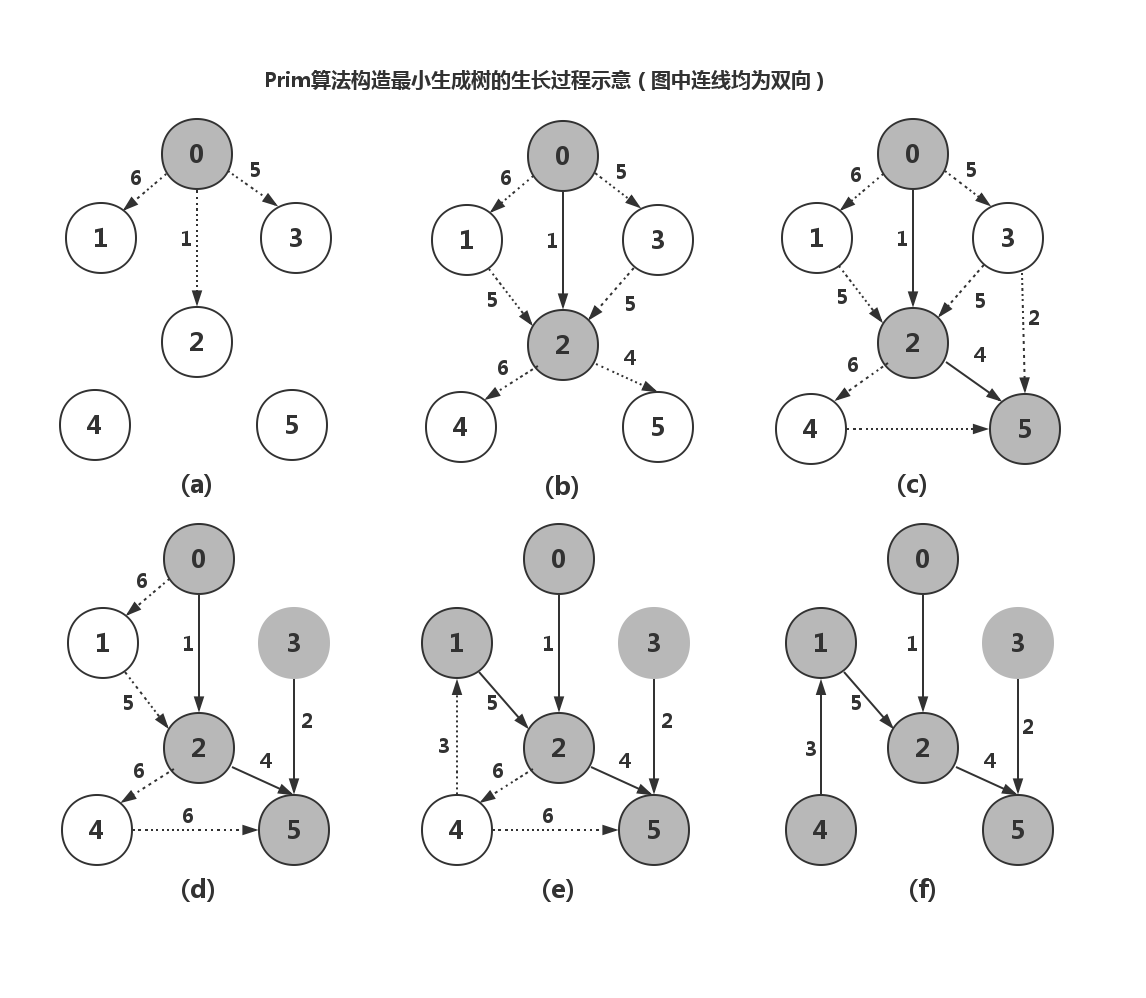 最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添
最小生成树(MinimumSpanningTree,MST)是一种图论算法,用于在一个带权重的无向连通图中找到一棵包括所有顶点且总权重尽可能小的树。常见的最小生成树算法有两种:Prim算法和Kruskal算法。Prim算法原理:Prim算法是一种贪心算法,它从图中的一个顶点开始,逐步增加边,每次都添 -
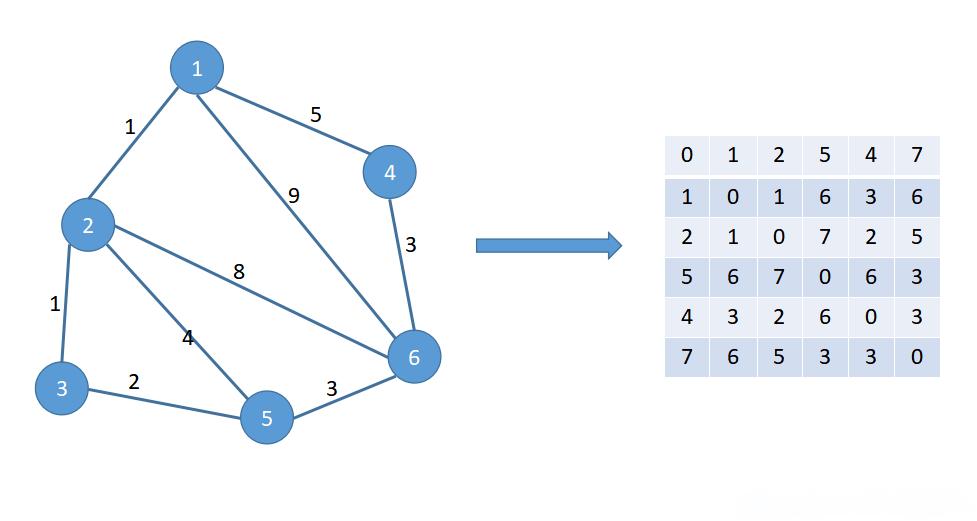 关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选
关于最短路径算法的Java实现,这里简述一下几种常用的算法及其基本原理,并给出一个Dijkstra算法的基本实现框架。Dijkstra算法(适用于无负权边的图)Dijkstra算法用于寻找图中一个顶点到其他所有顶点的最短路径。它维护了一个距离表,用来存储从源点到各个顶点的已知最短距离,并且每次都会选

